 wykresów sinusa i cosinusa nie potrafisz narysować
wykresów sinusa i cosinusa nie potrafisz narysować  no to masz problem
no to masz problem

 a)
y = sin 3x
−−−−−−−−−−−−−
Nierówność
sin 3x ≤ 0
π*k + π ≤ 3x ≤ 2π + π*k / : 3
a)
y = sin 3x
−−−−−−−−−−−−−
Nierówność
sin 3x ≤ 0
π*k + π ≤ 3x ≤ 2π + π*k / : 3
| π | π | 2 | π | ||||
+ | *k ≤ x ≤ | π + | *k , k − dowolna liczba całkowita | ||||
| 3 | 3 | 3 | 3 |
 a)
y = sin 3x
−−−−−−−−−−−−−
Nierówność
sin 3x ≤ 0
π*k + π ≤ 3x ≤ 2π + π*k / : 3
a)
y = sin 3x
−−−−−−−−−−−−−
Nierówność
sin 3x ≤ 0
π*k + π ≤ 3x ≤ 2π + π*k / : 3
| π | π | 2 | π | ||||
+ | *k ≤ x ≤ | π + | *k , k − dowolna liczba całkowita | ||||
| 3 | 3 | 3 | 3 |
 C − zbiór liczb całkowitych
sin 3x ≤ 0
Aby narysować wykres funkcji y = sin 3x trzeba znać własności wykresu funkcji y = sin x
(426).
Funkcja y = sin x ma wartości dodatnie, dla x∊(2kπ, π + 2kπ), k∊C, czyli dla 2kπ < x < π + 2kπ.
Podobnie ujemne dla x∊(−π + 2kπ, 2kπ), k∊C.
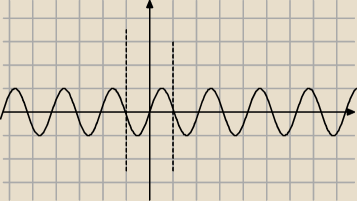
Teraz mamy funkcję y = sin 3x, Muszą być spełnione warunki.
Funkcja ma wartości dodatnie, dla: 2kπ < 3x < π + 2kπ, czyli:
23kπ < x < π3 + 23kπ; podobnie wartości ujemne −π3 + 23kπ < x <
23kπ.
Z taką wiedzą wiemy, że wykres funkcji będzie się powtarzał przedziałami od −π3 do π3
a okres podstawowy to 23π i łatwo narysować wykres. Z wykresu łatwo odczytać, że
sin3x ≤ 0 to x∊<−π3 + 23kπ, 23kπ>, k∊C
C − zbiór liczb całkowitych
sin 3x ≤ 0
Aby narysować wykres funkcji y = sin 3x trzeba znać własności wykresu funkcji y = sin x
(426).
Funkcja y = sin x ma wartości dodatnie, dla x∊(2kπ, π + 2kπ), k∊C, czyli dla 2kπ < x < π + 2kπ.
Podobnie ujemne dla x∊(−π + 2kπ, 2kπ), k∊C.
Teraz mamy funkcję y = sin 3x, Muszą być spełnione warunki.
Funkcja ma wartości dodatnie, dla: 2kπ < 3x < π + 2kπ, czyli:
23kπ < x < π3 + 23kπ; podobnie wartości ujemne −π3 + 23kπ < x <
23kπ.
Z taką wiedzą wiemy, że wykres funkcji będzie się powtarzał przedziałami od −π3 do π3
a okres podstawowy to 23π i łatwo narysować wykres. Z wykresu łatwo odczytać, że
sin3x ≤ 0 to x∊<−π3 + 23kπ, 23kπ>, k∊C