pomocy ada: Wydajność pracy ucznia szkoły średniej w ciągu dziesięciogodzinnego dnia pracy, po x godzinach dana jest wzorem: W(x)=−x³+6x²−9x+2. Uczeń rozpoczyna pracę o 8:00 rano. O której godzinie jego wydajność jest największa?

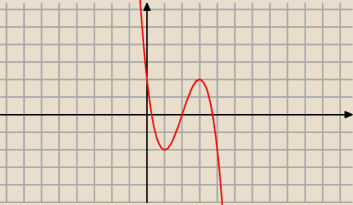
Saizou : D: 10>x>0 W'(x)=−3x²+12x−9=−3(x−3)(x−1) badamy znak wokoło argumentów 3 i 1 i wychodzi że − 1 + + 3 − rysujemy przybliżony wykres i widać że największą wartość w przedziale 10>x>0 jest dla x=3 zatem po 3 godzinach od rozpoczęcia zajęć jego wydajność jest największa, czyli o godzinie 11:00 czy jakoś tak

daras: GG:2489859 pobadaj te funkcję i znajdź maksimum https://matematykaszkolna.pl/strona/387.html

daras: pierwsza pochodna ma 2 miejsca zerowe: 1 i 3 a wartość drugiej pochodnej w tych miejscach jest f'(1)>0 i f'(3)<0 więc dla x = 3 ma lokalne maksimum

daras: ktoś mnie ubiegł ?

magda: dziękuję

ada: to ja dziękuję