Funkcja wymierna

Funkcja wymierna Radek:

	s
Wykres funkcji g otrzymano przesuwając wykres		o wektor v^→ Wyznacz wekroe v^→
	x

	−4x+1		−4(2x+1)+5		5		5
g(x)=		=		=−4+		=−4+
	2x+1		2x+1		2x+1		2(x+0,5)

	2,5
g(x)=		−4 v^→=[−0,5 −4] jednak to się nie zgada bo wykres po przekształceniach nie
	x+0.5

daje wykresu wyjściowego ?

3 lis 22:52

krystek:

−2(2x+1)+3		3
	=−2+
2x+1		2x+1

3 lis 23:02

Radek: Ale czemu moim sposobem jest źle ? Nie rozumiem tego ?

3 lis 23:03

krystek: −4(2x)=−8x

3 lis 23:04

Radek:

−4(2x+1)		5
	+		mam mnożenie więc skracam i mam −4 ?
2x+1		2x+1

3 lis 23:07

krystek: Ale ską to otrzymałeś ?

3 lis 23:08

Eta:

−2(2x+1)+3
	=.........
2x+1

3 lis 23:09

Radek: w miejsce x podstawiam mianownik ?

3 lis 23:10

Eta: Wymnóż w liczniku to co napisałeś U{−8x+1} ≠ −4x+1 wiesz już dlaczego ?

3 lis 23:11

krystek: Eto 22:02 zapisała zainteresowanemu ,ale tworzy swoja wersję.

3 lis 23:12

Saizou : https://matematykaszkolna.pl/forum/219169.html przepraszam że się wcinam ale ma ktoś chwilkę czasu

3 lis 23:12

Radek: Nic nie tworzę tylko chcę to zrozumieć a to jest różnica..

3 lis 23:13

Eta: Najprościej jest wykonać "zwykłe" dzielenie: ( unikniesz wtedy takich błędów (−4x+1 ) : (2x+1)= −2 4x+2 −−−− = 3 −−reszta

	3
zatem otrzymujesz: g(x)= −2+
	2x+1

3 lis 23:14

Radek: Pani Eto czyli jak mianownik byłby x+1

	−4x+1		−4(x+1)+5		5
g(x)=		=		=−4+
	x+1		x+1		x+1

po prostu chyba jak mam coś przy x to nie mogę wstawiać do licznika ?

3 lis 23:20

Eta: dokładnie emotka

3 lis 23:20

Radek: Danke emotka

3 lis 23:23

Eta: wykonując dzielenie.... bo wiesz,że kreska ułamkowa zastępuje znak dzielenia emotka

( −4x+1) : (x+1)= −4 4x+4 −−−−− = 5

	5
g(x)= −4+		i nie musisz myśleć , co dodać, a co odjąć, a co wyłączyć !
	x+1

powodzenia emotka

3 lis 23:24

Radek: Jeszcze takie pytanie jak ma Pani czas oczywiście jak rysować wykresy takich funkcji

	x+4		4
a) f(x)=\|		\| to rysuje normalne wykres		a następnie przesuwam o v^→[0,1] i to co
	x		x

pod osią nad oś ?

3 lis 23:27

Radek: Ale jak jeszcze określić dziedzinę tej funkcji ?

3 lis 23:32

krystek:

	x		4		4
I		+		I=I1+		I
	x		x		x

3 lis 23:34

krystek: D=R/{0}

3 lis 23:35

Eta: D_f = R\{0} i tak jak podałeś .......wykres jest ok emotka

3 lis 23:35

Radek: A takie coś:

	6
g(x)=
	\|x−2\|

rozpatrzeć w przedziałach ? x−2≠0 x≠2 D=R\{2} ?

3 lis 23:39

Eta:

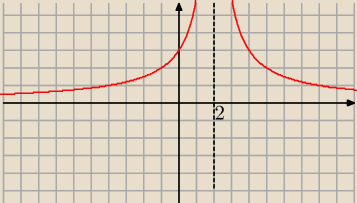
	6
tak : dla x > 2 f(x)=
	x−2

	6		−6
dla x<2 f(x)=		=
	−x+2		x−2

3 lis 23:43

Radek: Nie musiała Pani rysować emotka

Ale dziękuje wystarczyła tylko odpowiedź tak czy nie emotka

3 lis 23:46

Radek:

2x−\|x+1\|

x−1

D=R\{1} Też rozważam w przedziałach tak ?

3 lis 23:47

Eta: tak emotka

3 lis 23:49

Mila: O jak pięknie,że Eta dołączyła. Byłam u studenta. I Krystek też tu jest, pozdrowienia emotka

dla miłych Pań i ucznia też za pilność.

3 lis 23:50

Radek: Dziękuję emotka

3 lis 23:50

Eta:

3 lis 23:51

5-latek:

	6
I teraz dla x≥2 g(x)=
	x−2

	6		6		6
dla x<2 g(x)=		=		=
	−(x−2)		−x+2		2−x

3 lis 23:51

Eta: Ejjj "małolatku"

... x>2 , bo D_f : x≠2

3 lis 23:53

Radek: A Pani Eta niczym Strażnik Teksasu stoi i pilnuję porządku na forum emotka

3 lis 23:54

5-latek: Tak ma byc jak mowisz . Masz racje . Jednak juz pozno na pisanie . emotka

3 lis 23:56

Eta:

3 lis 23:58

Radek: rysunek

	1
Mam narysować wykres funkcji f(x)=		+3
	x−5

D=R\{5}

1
	v^→[5,3}
x

1
	i przesuwam o 5 jednostek w prawo i 3 do góry ale wtedy przetnie asymptotę ? Może ktoś
x

wyjaśnić ?

4 lis 00:06

Eta:

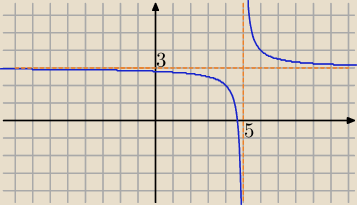
4 lis 00:11

Radek:

	1
A jak bez rysowania f(x)=		+3 określić ZW i monotoniczność ?
	x−5

Wiem, że późna pora ale matura

4 lis 00:12

Eta:

	1
f(x)=		+q
	x−p

ZW= y∊R \ {q}

4 lis 00:15

Radek: ZW=R\{3} a monotoniczność ? Wiem, że ta funkcja będzie albo malejąca albo rosnąca w przedziałach (−∞...) ,(...,∞) tylko co wpisać w miejsce kropek ?

4 lis 00:17

Eta:

	a
f(x) =		+ q
	x−p

dla a >0 f↘ dla x∊(−∞, p) , x∊(p, ∞) ( koniecznie "przecinek" bez znaku sumy

dla a<0 f↗ dla x∊(−∞, p) , x∊(p,∞)

4 lis 00:22

Radek: Napisałem przecinek, wiem, że tam nie ma znaku sumy bo to by była nieprawda emotka

4 lis 00:23

Eta: No i pięknie emotka

4 lis 00:24

Radek: Coś tam umiem, ale mam 26 listopada chodzi mi po głowie

4 lis 00:24

Eta: Wiem, wiem emotka

nie tylko Tobie "chodzi" Będzie dobrze .... do maja sporo czasu emotka

4 lis 00:26

Radek: Tak ale napisać roz na 40 czy mnie to raczej wstyd emotka

4 lis 00:27

Eta: Wstyd, to "kraść"

Rozwiązuj dużo zadań, a po północy ....... do spania

4 lis 00:28

Radek: Ale ja nie odczuwam na razie potrzeby spania emotka

w dwa−trzy dni robie jeden dział z kiełbasy emotka

4 lis 00:29

Eta: Pora do spania emotka

Miłych snów emotka

4 lis 00:46

Radek: W takim razie dobranoc emotka

Ale pora jest do robienia zadań

4 lis 00:47