przeksztalcenia zadanie: teraz troche algebry liniowej a dokladniej przeksztalcenia plaszczyzn 1. Translacja zadana jest wzorami x'=x+1 i y'=y−3. Jakie punkty będą obrazami punktów (0,0), (1,0) przez tą translacje? A jakie punkty będą przekształcone na te punkty? A(0,0) x'=0+1=1 y'=0−3=−3 A'(1,−3); punkt A' jest obrazem punktu A przez ta translacje B(1,0) x'=1+1=2 y'=0−3=−3 B'(2,−3); punkt B' jest obrazem punktu B przez ta translacje dobrze? A jakie punkty będą przekształcone na te punkty? nie rozumiem tego pytania?

Basia: masz znaleźć takie M i N, żeby obrazem M był A, a obrazem N był B czyli M(x,y) nieznane natomiast x'=0 i y'=0 N(x,y) nieznane natomiast x'=1 i y'=0 podstawiasz i wyliczasz x,y

zadanie: czyli odwrotnie do poprzedniego? a tamto dobrze ?

Basia: tak; dobrze

zadanie: dziekuje

Mila: w^→=[1,−3] −w→=[−1,3] A=(0,0)→T_[−1,3]→A"=(0+(−1),0+3)=(−1,3) B=(1,0)→T_[−1,3]→B"=(1+(−1),0+3)=(0,3)

Mila: Witaj Basiu. zerknij na sumę z gdodziny19:20. https://matematykaszkolna.pl/forum/218934.html

zadanie: 2. Wylicz posługując się wzorami przekształcenie odwrotne do przesunięcia o wektor [−2,3]. Odczytaj z uzyskanego wzoru jakie to przekształcenie. tego nie rozumiem w ogole moglbym prosic o wytlumaczenie?

Basia: przekształceniem odwrotnym do translacji o wektor [u;v] odwrotna jest translacja o wektor [−u; −v]

Mila: Dane przekształcenie; x'=x−2 y'=y+3 Przekształcenie odwrotne: x=x'+2 y=y'−3 Teraz możesz zamienić znaczki x'=x+2 y'=y−3 to jest przekształcenie o wektor [2,−3] Zobacz na rysunek i rachunki 22:52

zadanie: dziekuje a jak zmienia sie te wspolrzedne? to tez jest dla mnie klopotliwe

Mila: Nie wiem o co Ci chodzi?

zadanie: no bo w tych przeksztalceniach zamienia sie wspolrzedne a skad mam wiedziec kiedy to zrobic?

Mila: Jeżeli wektor u^→jest równy [a,b], to obrazem punktu P(x,y) w translacji o wektor u^→=[a,b] jest taki punkt P'(x',y') ,że x'=x+a y'=y+b współrzędne punktu po przesunięciu o wektor [a,b] np. A=(2,3) i u^→[5,1] A=(2,3)→T_[5,1]=A'=(2+5,3+1)=(7,4) Zadanie. wykaż, że translacja zachowuje prostopadłość prostych.

zadanie: jeszcze wroce do zadania 1. a konkretnie do pytania: A jakie punkty beda przeksztalcone na te punkty? co znaczy przeksztalcone ? no bo na te punkty czyli na punkty A(0,0) i B(1,0) pierwsza czesc zadania rozumiem. jest dany wzor tej translacji (przesuniecia) z niego mozna odczytac wektor [1,−3] i mamy znalezc obrazy punktow A(0,0) i B(1,0) w przesunieciu o wektor [1,−3]. czyli tymi punktami sa: A'(1,−3) jest on obrazem punktu A(0,0) i B'(2,−3) jest on obrazem punktu B(1,0). a tego drugiego pytania nie rozumiem. nie moge sobie tego wyobrazic.

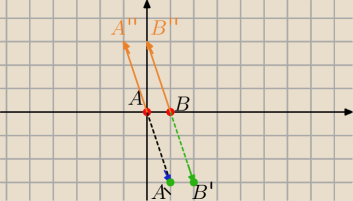
Mila: No nie wiem , dlaczego nie wpisał się rysunek. Zaraz narysuję. Przesunięto punkty A i B o wektor [1,−3] i otrzymaliśmy punkty A' i B' . II problem, Jakie punkty przesunięto o wektor [1, −3], ze otrzymano punkty A i B. Przesuwam punkty A i B równolegle w przeciwną stronę , czyli o wektor [−1,3] i otrzymuję A"=(−1,3) i B"=(0,3) Jeżeli teraz dokonasz translacji A" i B" o wektor [1,−3], to właśnie otrzymasz A i B.

zadanie: dziekuje bardzo nad tym zadaniem sprobuje pomyslec jutro teraz ide juz spac

Mila: Czy zrozumiałeś o co chodzi w tej translacji? To najłatwiejsze przekształcenie, zaraz będziesz miał trudniejsze.

zadanie: tak teraz juz rozumiem juz mam trudniejsze tylko na liscie byly zadania z translacja jutro dalej bede probowac je robic przeksztalcenia odwrotne i zlozenia tego za bardzo nie rozumiem jak zamieniac te wsporzedne ale to ewentualnie jutro

zadanie: jezeli chodzi o przeksztalcenia odwrotne to nie zawsze one istnieja istnieja, gdy przeksztalcenie T jest wzajemne jednoznaczne (czyli roznowartosciowe i ''na''). moglibysmy zrobic 2 przyklady obrazujace to przeksztalcenie odwrotne? 1 przyklad, gdzie to przeksztalcenie istnieje a 2, gdzie nie istnieje i dlaczego? i w tym przykladzie, gdzie istnieje poprosilbym o wytlumaczenie kiedy zamienia sie te wspolrzedne .

zadanie: ja bede po 18 bo dzisiaj wracam

zadanie: juz jestem

zadanie: moglbym prosic o przyklady ?

zadanie: ?

Mila: Zadanie1. Wykaż, że translacja zachowuje prostopadłość prostych. Jeśli chodzi o przykłady, to chyba nie będą odpowiednie z moich zbiorów.

Mila: Zadanie 2. Sprawdź ,że istnieje translacja, w której obrazem czworokąta o wierzchołkach: A=(−2,−1),B=(2,−1),C=(2,1),D=(−2,1) jest czworokąt o wierzchołkach: K(1,1), L(5,1),M(5,3),N(1,3). zadanie 3. Zbadaj, czy przekształcenie płaszczyzny dane wzorami: x'=−2y y'=2x a) jest izometrią b) znajdź punkty stałe tego przekształcenia.

zadanie: zadanie 1. zalozmy, ze mamy prosta a i na niej dwa punkty A i B liczymy wektor AB potem przesuwamy te punkty o wektor u=[m.n] gdy mamy wspolrzedne nowych punktow A' i B' to liczymy wektor A'B' i potem obliczamy iloczyn skalarny tych wektorow powinien wyjsc 0 , zeby byly prostopadle ale mi nie wychodzi 0 natomiast gdy oblicze wyznacznik to wychodzi 0 czyli sa rownolegle na prostopadlosc nie mam pomyslu

zadanie: zadanie 2. a, b− wspolrzedne wektora u K(1,1) x'=1 y'=1 korzystajac ze wzorow na translacje mam: a=1+2=3 b=1+1=2 czyli u=[3,2] L(5,1) a=5−2=3 b=1+1=2 taki sam wektor M(5,3) a=5−2=3 b=3−1=2 taki sam wektor N(1,3) a=1+2=3 b=3−1=2 taki sam wektor istnieje translacja o wektor u=[3,2].

zadanie: zadanie 3. a) izometria jest wtedy, gdy zachowuje odleglosc pomiedzy punktami A(x_a,y_a), B(x_b, y_b) A'(−2y_a, 2x_a), B'(−2y_b, 2x_b) odleglosc punktow A i B wynosi IABI=√(x_b−x_a)²+(y_b−y_a)² odleglosc punktow A' i B' wynosi IA'B'I=√−2x_b+2x_a)²+(2y_b−2y_a)² odleglosc nie jest taka sama wiec nie jest to izometria

Mila: Zadanie 1) p₁: y=mx+n

	−1
p2: y=		x+k i p1⊥p2
	m

u^→=[a,b] x'=x+a y'=y+a stad x=x'−a i y=y'−b podstawiamy do równań prostych p1': y'−b=m*(x'−a)+n⇔y'=mx'−ma+n+b

	−1		−1		a		−1
p2': y'−b=		(x'−a)+k⇔y'=		*x'+		+k+b⇔m*		=−1
	m		m		m		m

p1'⊥p2'

Mila: Zadanie 2) dobrze. Zadanie 3) punkt stały , to znaczy T(P)=P P(x,y) x'=−2y y'=2x x'=x⇔x=−2y y'=y⇔y=2x ⇔y=2*(−2y)⇔5y=0, x=0 (0,0) punkt stały tego przekształcenia spr. x'=−2*0=0 y'=2*0=0

Mila: 3a) dobrze.

zadanie: b) jezeli nie jest to izometria to pozostaje jednokladnosc punktem stalym jednokladnosci jest srodek jednokladnosci

zadanie: dziekuje

zadanie: Punkt A(1,1) przechodzi przez przesuniecie na punkt A'(−1,0). Na jaki punkt przejdzie przez to przesuniecie poczatek ukladu? trzeba wyliczyc wspolrzedne wektora zgodnie ze wzorami na translacje v=[−2,−1] O(0,0) x'=−2 y'=−1 O'=(−2,−1) przejdzie na punkt O' dobrze?

Mila: Nie było pytania jakie to przekształcenie, ale czy izometria. To nie jest jednokładność.

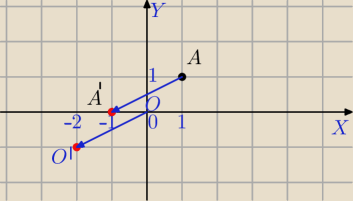
Mila: Wektor translacji AA'^→[−1−1,0−1]=[−2,−1] Musisz "widzieć" te wektory. Rysuj układ współrzędnych i zaznaczaj punkty, jeśli tylko da się.

zadanie: Dane jest przeksztalcenie x'=x+2y, y'=y+3. Znajdz obrazy kilku wybranych przez siebie punktow przez to przeksztalcenie. Jakie punkty sa przeksztalcane na te wybrane przez ciebie punkty? Znajdz wzor przeksztalcenia odwrotnego. Znajdz wzor zlozenia tego pzeksztalcenia z translacja dana wzorem x'=x+1, y'=y−3. Znajdz rownania obrazow krzywych 2x−y−1=0, x²+y²=1 oraz y=x² przez to przeksztalcenie.

zadanie: chcialbym zrobic to zadanie zaraz napisze pierwsza czesc zadania do sprawdzenia

zadanie: wracajac do zadania z izometria jezeli nie jest to izometria ani jednokladnosc to jakie to przeksztalcenie? da sie to okreslic na podstawie podanego wzoru?

zadanie: Wybrane punkty: A(2,−5), B(1,−4), C(0,3) Obrazy tych punktow: A' x'=2+2*(−5)=−8 y'=−5+3=−2 stad A'(−8, −2) podobnie pozostale czyli B'(−7,−1) i C'(6,6). Jakie punkty sa przeksztalcane na te wybrane przez ciebie punkty? wczoraj bylo podobne ale z wektorem a tutaj? A''=(−2y,−3) czyli A''=(10, −3) ? Wzor przeksztalcenia odwrotnego: Dane przeksztalcenie: x'=x+2y y'=y+3 Wyliczam x i y: x=x'−2y y=y'−3 zamieniam x' na x oraz y' na y Ostatecznie wzor przeksztalcenia odwrotnego: x'=x−2y y'=y−3 dobrze?

zadanie: niech T₁: x'=x+2y oraz T₂: x'=x+1 y'=y+3 y'=y−3 T₂◯T₁=T₂(T₁)=T₂(x+2y, y+3)=(x+2y+1, y+3−3)=(x+2y+1, y) Wzor zlozenia : x'=x+2y+1 y'=y dobrze?

Mila: Sprawdzam.

Mila: 22:18 dobrze. Rozwiązuj dalej.

zadanie: rownania obrazow krzywych nie wiem czy dobrze to robie wiec napisze jedno rownanie krzywej: 2x−y−1=0 x=x'+2y y=y'+3 wstawiam to do rownania krzywej: 2(x'+2y)−(y'+3)−1=0 2(x'+2(y'+3))−(y'+3)−1=0 zamieniam x' na x i y' na y 2x+3y+8=0 dobrze?

zadanie: a to z godz. 21:55 dobrze?

zadanie: jezeli sa jakies bledy to poprosilbym o dokladne wytlumaczenie

Mila: T₁: x'=x+2y, y'=y+3. Obrazem punktu A(2,−5) jest punkt A'=(−8,−2) Punkt A jest obrazem punktu: A"(x,y), szukamy wsp.(x,y) 2=x+2y −5=y+3⇔y=−8 2=x+2*(−8) 2=x−16 x=18 A"=(18,−8) ========== spr. x'=18+2*(−8)=18−16=2 y'=−8+3=5 Punkt A jest obrazem punktu A"=(18,−8) ============================

Mila: Ostatecznie wzor przeksztalcenia odwrotnego: x'=x−2y y'=y−3 dobrze Miałeś przekształcić krzywe wg złożenia. k1: 2x−y−1=0, k2: x²+y²=1 oraz y=x² Wzór złożenia : x'=x+2y+1 ⇔x=x'−2y−1 y'=y a) k1: b) k2: (x'−2y−1)²+y'²=1 (x'−2y'−1)²+y'²=1⇔x²−4xy−2x+5x²+4y=0 c) y=x² y'=(x'−2y'−1)² x²−4xy−2x+4x²+4y+1=0

zadanie: dziekuje

Mila: Napisz,jak na zajęciach będzie innym sposobem.

zadanie: dobrze

zadanie: mam jeszcze pytanie czy skladania przeksztalcen zawsze mozna dokonac?

zadanie: ?

Oliv: Dlaczego to przekształcenie krzywych robimy względem złożenia, a ni względem tego przekształcenia co jest na początku zadania?