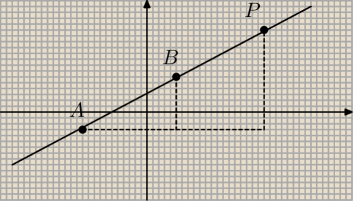
 Zakładam, że prosta nie jest ani pionowa, ani pozioma
A=(xA, yA)
B=(xB; yB)
P=(x; y)
Zakładam, że prosta nie jest ani pionowa, ani pozioma
A=(xA, yA)
B=(xB; yB)
P=(x; y)
| y−yA | yB−yA | ||
= | |||
| x−xA | xB−xA |
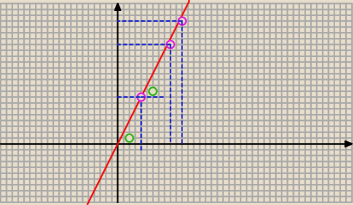 A = ( xA, yA ) B = ( xB ; yb ) oraz P = ( x; y)
więc
Punkty A , B i P leżą na jednej prostej , gdy wektory
→ →
AP i AB są równoległe czyli gdy spełniają warunek :
( x − xA) *( yB − yA) − ( xB − xA)*( y − yA) = 0
lub inaczej
( xB − xA)*( y − yA) = ( x − xA)*( yB − yA)
lub jeszcze inaczej ( po podzieleniu przez x B − xA )
A = ( xA, yA ) B = ( xB ; yb ) oraz P = ( x; y)
więc
Punkty A , B i P leżą na jednej prostej , gdy wektory
→ →
AP i AB są równoległe czyli gdy spełniają warunek :
( x − xA) *( yB − yA) − ( xB − xA)*( y − yA) = 0
lub inaczej
( xB − xA)*( y − yA) = ( x − xA)*( yB − yA)
lub jeszcze inaczej ( po podzieleniu przez x B − xA )
| yB − yA | ||
y − yA = | * ( x − xA) | |
| xB − xA |
| yB − yA | ||
a = | = tg α − współczynnik kierunkowy prostej | |
| xB − xA |
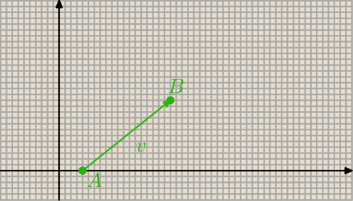 A=(xA,yA)
B=(xB,yB)
dwa punkty połączone w odcinek utworzą wektor AB=[ Bx−Ax, By−Ay]
( Bx−Ax )( y − Ay ) = ( By−Ay )( x − Ax ) wzór do którego dojdziemy :
RÓWNANIE PROSTEJ
X=A+tV
X − punkt należący do tej prostej, X=[x,y] ;
A punkt należący do prostej A=[Ax,Ay],
t ∊ℛ t− pewna liczba dla ułatwienia rachunków
przyjmijmy 1
V wektor(Bx−Ax, By−Ay) utworzony dwóch punktów A i B ; wektor AB=V ,
punkt początkowy−−> A ,
x=Ax+tVx ==> x−Ax=Vx wiemy że V=(Bx−Ax, By−Ay)
y=Ay+tVy ===>y−Ay=Vy
A=(xA,yA)
B=(xB,yB)
dwa punkty połączone w odcinek utworzą wektor AB=[ Bx−Ax, By−Ay]
( Bx−Ax )( y − Ay ) = ( By−Ay )( x − Ax ) wzór do którego dojdziemy :
RÓWNANIE PROSTEJ
X=A+tV
X − punkt należący do tej prostej, X=[x,y] ;
A punkt należący do prostej A=[Ax,Ay],
t ∊ℛ t− pewna liczba dla ułatwienia rachunków
przyjmijmy 1
V wektor(Bx−Ax, By−Ay) utworzony dwóch punktów A i B ; wektor AB=V ,
punkt początkowy−−> A ,
x=Ax+tVx ==> x−Ax=Vx wiemy że V=(Bx−Ax, By−Ay)
y=Ay+tVy ===>y−Ay=Vy
| (x−Ax) | ||
podstawiamy (x−Ax)=(Bx−Ax) ==> | =0 | |
| (Bx−Ax) |
| (y−Ay) | ||
(y−Ay)=(By−Ay) ==> | =0 STĄD : | |
| (By−Ay) |
| (x−Ax) | (y−Ay) | ||
= | NA SKOS | ||
| (Bx−Ax) | (By−Ay) |
