Rozwiąż równanie
Dexter: Rozwiąż równanie:
|x| + |x + 5| = 2x + 5
27 paź 13:05
27 paź 13:08
Dexter: Już tam byłem, w sumie to mam problem tylko z jednym fragmentem:
Czy dla tego przedziału − x∊(−∞,−5)
|x| = x czy |x| = − x
Mógłbyś mi to wyjaśnić?
27 paź 13:19
john2: Jeśli podstawisz za x jakąś liczbe z tego przedziału, to będzie to liczba ujemna czy nieujemna?
27 paź 13:21
john2: Będzie to liczba ujemna. dlatego przy opuszczaniu wartości bezwzględnej trzeba dać minus przed
x, w ten sposób upewniamy się, że nasze wyrażenie po opuszczenie modułów jest nieujemne, bo
dwa minus dadzą plus
https://matematykaszkolna.pl/strona/15.html
27 paź 13:24
Dexter: x − liczba ujemna
|x| − liczba nieujemna
Zgadza się?
27 paź 13:24
john2: W tym przedziale, tak
27 paź 13:26
john2: Najlepiej to widać tutaj
https://matematykaszkolna.pl/strona/1091.html
W drugim przykładzie, nasze wyrażenie między kreskami okazuje się
ujemne, dlatego przy opuszczaniu wartości bezwzględnej trzeba dać przed tym wyrażeniem minus,
w ten sposób upewniamy się, że mamy wyrażenie dodatnie, bo wartośc bezwzględna musi być
dodatnia
27 paź 13:29
Dexter: Czyli dla przedziału x∊(−∞,4)
|x| jest x
a dla x∊(−∞,−1)
− |x| = −x
27 paź 13:29
john2: hmm z tym pierwszym przedziałem byłby problem, bo x (nasze wyrażenie w module) może być zarówno
ujemne jak i dodatnie
na pewno dobrze przedziały ustaliłeś?
w drugim po prostu |x| = −x
27 paź 13:32
john2: mi wychodzą takie przedziały
1) x∊ (−∞,−5)
2) x ∊ <−5,0)
3)x ∊ <0, +∞)
27 paź 13:35
Dexter: W pierwszym przykładzie jest to jeden z przedziałów z |x| − |x − 4| = 2
Drugi przykład to jeden z przedziałów z |x + 1| − |x| = 0
27 paź 13:36
Dexter: Rozumiesz czy niezbyt?
27 paź 13:43
john2: przedziały w |x| − |x −4| = 2
1) x ∊ (−∞,0)
2) x ∊ <0,4)
3 x∊<4, +∞)
przedziały w |x + 1| − |x| = 0
1) x ∊ (−∞, −1)
2) x ∊ <−1,0)
3) x∊<0,+∞)
27 paź 13:44
john2: Każdy z tych przedziałów jasno nam powie czy x w |x| jest ujemny czy nieujemny, nie będzie
sytuacji, że możesz za x podstawić liczbę dodatnia, i jednocześnie ujemną
27 paź 13:45
john2: przykładowo w pierwszym zadaniu 1) Masz przedział ze wszystkimi liczbami ujemnymi, więc wiesz,
że musisz dać przed x minus przy opuszczaniu wartości bezwzględnej, aby uczynić nasze
wyrażenie dodatnim
27 paź 13:48
Trivial:
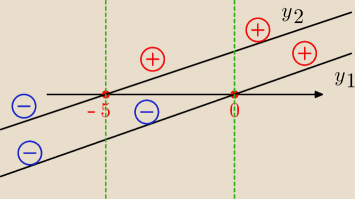
27 paź 13:50
pigor: ..., Rozwiąż równanie:
|x|+|x+5|= 2x+5 , np.
tak :
|x|+|x+5|= 2x+5 ⇒ [|x|+|x+5|= 2x+5 i 2x+5 ≥0 ⇔ x ≥ −2,5 i |x|+x+5= 2x+5 ⇔
⇔ x ≥ −2,5 i |x|= x ⇔ x ≥−2,5 i x ≥0 ⇔
x ≥0 ⇔
x∊[0;+∞) i to tyle. ...

27 paź 13:55
Dexter: Czyli już chyba wiem, co robiłem źle.
Przy np. takich równaniach |x| + |x + 5| = 7
Nie robię tylko dwóch przedziałów: 1) x∊(−∞,−5) oraz 2) x∊<−5,∞), a robię trzy przedziały
1) x∊(−∞,−5) 2) x∊<−5,0) 3) x∊<0,∞)?
27 paź 13:59
john2: Tak, musisz podzielić całą rzeczywistość na przedziały, nie pomijając ani jednego punktu
27 paź 14:10
john2: i nie pomijając miejsc zerowych
27 paź 14:11
Dexter: No to rozumiem

, a ja przez cały czas robiłem dwa przedziały i wychodziły mi złe rozwiązania.
Wielkie dzięki za pomoc i spędzenie nad moim problemem prawie godziny

27 paź 14:17


 , a ja przez cały czas robiłem dwa przedziały i wychodziły mi złe rozwiązania.
Wielkie dzięki za pomoc i spędzenie nad moim problemem prawie godziny
, a ja przez cały czas robiłem dwa przedziały i wychodziły mi złe rozwiązania.
Wielkie dzięki za pomoc i spędzenie nad moim problemem prawie godziny