Funkcja ? Kostek: Jednym z miejsc zerowych funkcji kwadratowej f jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to <2 ,+∞ ) . Największa wartość funkcji f w przedziale <− 8,− 7> jest równa (− 24) . Wyznacz wzór funkcji f x_w=2 y=a(x−5)(x−1) ale to za mało co robić dalej ?

Lorak: f(−7)=−24

ICSP: w przedziale <−8 ; −7> funkcja jest rosnąca czy malejąca ?

Kostek: rosnąca

Lorak: w przedziale (−∞;2] jest rosnąca, więc dla przedziału [−8;−7] największa wartość będzie w −7

Lorak: zamiast w −7 powinienem napisać dla x=−7

Kostek: Why?

Lorak: o co teraz pytasz?

Kostek: Czemu będzie to −7 ?

Lorak: na pewno wyznaczałeś kiedyś wartość minimalną i maksymalną funkcji kwadratowej w danym przedziale, przypomnij sobie

Kostek: Tak ale miałem podany wzór ..

Lorak: Chodzi o sam sposób. Funkcja rośnie, czyli dla coraz większych argumentów przyjmuje coraz większe wartości. W przedziale <−8;−7> największym argumentem jest −7, więc to dla niego wartość wyniesie −24

Kostek: ok danke

Lorak:

Kostek: Ale zastawiając się również dla −8 to może być −24 a dla −7 już np −22 ?

Lorak: nie bardzo wiem co masz na myśli.

Kostek: Tam mam podane, że wartość w tym przedziale wynosi −24 i powiedziałeś że dla argumentu −7 a może taką wartość przyjmuję dla −8 a dla −7 jest inna ?

Lorak: Największa wartość wynosi −24

Kostek: Ale nie wiadomo dla jakiego argumentu

Lorak: Nie potrafię inaczej Ci tego wytłumaczyć. Może rysunek pomoże w zrozumieniu. Zaraz jakiś przygotuję.

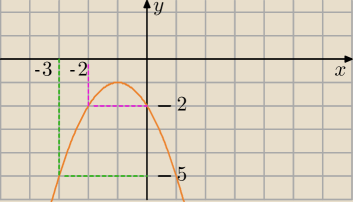
Lorak: w przedziale <−3;−2> największa wartość równa −2 przyjmowana jest dla największego argumentu z tego przedziału równego −2

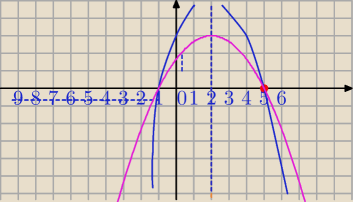
Mila: szkicujemy sytuację: niebieski kolor widzimy, że f(−8)<f(−7) w takim razie f(−7)=−24

	−b		−b
xw=		⇔2=		⇔b=−4a
	2a		2a

wykres jest symetryczny względem prostej x=2 stąd f(5)=f(−1)=0 f(−7)=−24 f(x)=a(x−5)*(x+1) a*(−7−5)*(−7+1)=−24 a*(−12)*−6=−24

	24		1
a=−		=−
	72		3

	1
f(x)=−		*(x−5)*(x+1)
	3

================== II sposób f(x)=ax²−4ax+c f(5)=a*5²−4a*5+c=0⇔25a−20a+c=0⇔5a+c=0 f(−7)=a*(−7)²−4*(−7)+c=−24⇔77a+c=−24⇔

	5
72a=−24 i c=
	3

	−1
a=
	3

	−1		4		5
f(x)=		x2+		x+
	3		3		3

=========================

Kostek: Dziękuję !

Mila: Zrozumiałeś?

bezendu: Tak, robię zadania z funkcji kwadratowej ale mam problem z niektórymi z podstawy nawet jak widać

bezendu: sorry nie tu

Mila: To gdzie jesteś Bezendu?

bezendu: https://matematykaszkolna.pl/forum/216866.html to miało być do tego k?