Funkcja bezendu: Kolejny raz przerosła mnie funkcja kwadratowa Wyznacz wartości parametru m, dla których funkcja f(x)=(m²−3)x²−8mx+5 jest rosnąca w przedziale (−∞,2>, a malejąca <2.∞) m²−3<0 (m−√3)(m+√3) m∊(−√3, p[3})

8m
	=2
2(m2−3)

8m
	=2
2m2−6

8m=4m²−12 4m²−8m−12=0/4 m²−2m−3=0 Δ_m=16 √Δ_m=4

	2−4
m1=		=−1∊(−√3.√3)
	2

	2+4
m2=		=3∉(−√3,√3)
	2

Piotr 10: bezendu na pewno m²− 3 <0

bezendu: No właśnie nie ogarniam

Piotr 10: Czekaj bo nie do końca przeczytałem zadanie

Piotr 10: OK. Czyli będzie to ogółem funkcja malejąca. Więc m²− 3 < 0

Lorak: Sposób jest OK, obliczeń nie sprawdzałem, ale też wyglądają w porządku.

Lorak: bezendu, rysunek pomocniczy zawsze pomaga w zrozumieniu.

Piotr 10:

bezendu: Lorak wiem właśnie sobie narysowałem parabolę Zaraz kolejne

Piotr 10: Jakby co to pisz pomożemy Ci . Funkcja kwadratowa nie jest trudna

bezendu: Dla jakich wartości parametru m prost o równaniu y−3x−m=0 ma z parabolą o równaniu y=x²+2x−3 ma dokładnie jeden punkt wspólny y=3x+m y=x²+2x−3 3x+m=x²+2x−3 x²−x−3−m=0 1−4(−3−m)=0 1+12+4m=0 4m=13

	13
m=		?
	4

Piotr 10:

	13
m= −
	4

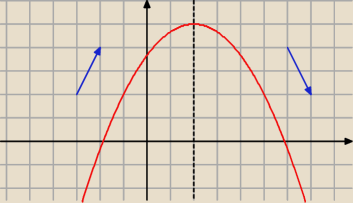
Trivial: Warunki zadania spełnia każda parabola postaci: A(x−2)² + B, A < 0, B dowolne Zatem: Ax² − 4Ax + (4A + B)

⎧	4A + B = 5
⎨	4A = 8m
⎩	A = m2−3

Zatem: 2m = m² − 3, A < 0 ⇒ m < 0 (m+1)(m−3) = 0 m = −1 ← jedyna odpowiedź < 0.

Lorak: bezendu, teraz masz 2 przecięcia. parabola rośnie szybciej niż funkcja liniowa. chyba jedyna opcja żeby było jedno przecięcie, to musi być ono w wierzchołku paraboli.

bezendu: Trivial czyli dobrze zrobiłem to pierwsze zadanie ?

Lorak: dobrze bezendu zrobiłeś pierwsze, trochę pewności siebie

Piotr 10: Pewnie, że tak

bezendu:

	13
A drugie ? Tylko tam powinno być −
	4

Trivial: Tak, przecież wyszło to samo.

Trivial: drugie K.

Lorak: moje rozumowanie z 19:46 jest złe, przekombinowałem. Nie czytaj

bezendu: drugie ''k'' ?

Trivial: Drugie "K"!

daras: jest to parabola, która ma wierzchołek w punkcie x = 2

daras: oczywiście odwrócona do góry dnem, ale widac miałem za długo okienko nie odświeżane bo oglądałem wiadomości i Trivial to już ładnie namalował