Sprawdzenie (logika) Nadia: Witam będe tu wstawiać zadania przygotowujące mnie do kolokwium . Proszę o sprawdzenie/ewentualną pomoc. 1 zadanie Czy jest to tautologia (p v (q⇒~p)) ⇔(p∧~q) Wyszło mi że nie jest to tautologia

Garth: Poprawnie. http://www.wolframalpha.com/input/?i=%5Bp+or+%28q+%3D%3E+~p%29%5D+%3C%3D%3E+%28p+and+~q%29

Nadia: Czyli dobrze zrobiłem że nie jest to tautologia?

Garth: Zgadza sie. W podanym przeze mnie linku jest podana skrocona tabelka reprezentujaca metode zero−jedynkowa dla danego schematu zdaniowego. Dla naszego przykladu mamy tam widoczna informacje, ze schemat ten jest prawdziwy tylko dla jednej sytuacji, a dla pozostalych trzech jest falszywy [a powinien byc prawdziwy dla wszystkich czterech sytuacji, by byla to tautologia]. Wnioskujemy wiec, ze nie jest to tautologia.

Nadia: 2 zadanie: A=(−∞,2) u <3,6) B= 2 do potęgi x−1 ≤4 No to z 2 wyszło że x≤3 I trzeba zaznaczyć A∩B B\A i B" (prim) A∩B wyszło mi (−oo,2)u ( i liczba 3) B" (3,6) B\A (2,3)

PuRXUTM: ja to sobie rozpiszę, napiszcie czy wszystko poprawnie bo też będę miał kolokwium kiedyś tam z logiki (p v (q⇒~p)) ⇔(p∧~q) (p v (¬q v ¬p)) ⇔ (p ∧~q) z łączności alternatywy mamy ((p v ¬p) v ¬q ) ⇔ (p ∧~q) (p v ¬p) możemy pominąć bo to zawsze prawda ( tak jest ? jak mamy zapisać to poprawnie na kolokwium ) dochodzimy do: ¬q ⇔ (p ∧~q) tu wystarczy podać kontrprzykład że to nie jest zawsze spełnione np. q=0 p=0 wtedy to nie jest tautologia

Garth: PuRXUTM, nie jestem pewien, czy na pewno bedzie to poprawne, ale ja bym zapisal tak: [(p ∨ ¬p) ∨ ¬q] ⇔ 1 ∨ ¬q ⇔ 1 Nadia, jakie sa zalozenia co do zbioru B? Czy maja to byc liczby rzeczywiste?

Nadia: ja to rozpisuję tak p|q|~p| ~q |q⇒~p |p v q⇒~p| p ∧~q| i całosc lacznie ⇔

Nadia: rzeczywiste

Garth: B\A, tutaj nalezaloby jeszcze dwojke wlaczyc.

Garth: B' to bedzie raczej rowny (3, ∞)

PuRXUTM: dzięki Garth

Garth: Ale zaznaczam, moge sie mylic co do formalnosci tego zapisu.

Nadia: o dzięki rzeczywiście B\A i B' powinny być tak jak ty piszesz Zapisać zaprzeczenie podanego zdania bez symbolu negacji i określić jego wartość logiczną ( odpowiedz uzasadnić) ( |x| < 1⇒ x² − x <0) A tego zadania kompletnie nie rozumiem ? Będzie super jeśli chociaż jakoś mnie naprowadzicie

Garth: To nie zabrzmialo zbyt dobrze...co do poprawnosci pod katem formalnym tego zapisu...juz lepiej.

PuRXUTM: Garth zerkniesz na moje zapytania https://matematykaszkolna.pl/forum/217798.html

Garth: Nadia, moge sie mylic, wiec dobrze by bylo, zeby ktos jeszcze to osadzil. p⇒q ⇔ ¬p ∨ q [prawo eliminacji implikacji] (|x| < 1 ⇒ x² − x < 0) A wiec zaprzeczenie bez uzycia negacji przy wykorzystaniu prawa eliminacji implikacji. (|x| ≥ 1 ⇒ x² − x < 0) Dobrze by bylo, zeby ktos to jeszcze sprawdzil. A poza tym to co i gdzie studiujesz?

Garth: Oj raczej Ci nie pomoge PuRXUTM. Ja tez dopiero na pierwszym roku jestem. Niby cos tam umiem granice, ale tak na bardzo podstawowym poziomie i ostatnio mialem z nimi przerwe [na uczelni na razie ich nie bierzemy, pewnie dopiero za miesiac czy dwa zaczniemy], wiec wole Ci zle nie doradzac.

PuRXUTM: ok A gdzie studiujesz

Garth: Politechnika Rzeszowska. A Ty?

Nadia: Politechnika Łódzka Inżynieria Środowiska. No kolega tak samo przedstawił to zadanie jak ty więc chyba jest to poprawne

PuRXUTM: UJ Kraków

Garth: No to poziom raczej wyzszy tam macie, z reszta jak patrzylem na te zadania, ktore tu wstawiasz, to raczej na pewno. Nadia, na tej Inzynierii macie osobny przedmiot jak logika, czy tez jakos inaczej jest to zorganizowane? Tak z ciekawosci tylko pytam.

Garth: Zle tam napisalem, jesli juz to powinno byc: (|x| ≥ 1 ∨ x² − x < 0)

PuRXUTM: no na razie jest masakra, ale nie ma co o tym myśleć trzeba zadanka robić

Nadia: Jeszcze ostatnie zadanie . Przedstawić graficznie zbiór .. wiem że tu raczej się go nie narysuje ale chodzi o rozwiązanie samo x²+4x+y²≤0⋀|x+2|<y Więc tak pierwsze równanie to równanie okręgu ? (x+2)² − 4 +y²=0 Czyli (x+2)² + y²=4 Czyli środek (−2,0) a promień 2 a jak to się rozwiązuje |x+2|<y X+2<y i X+2 > − y

Garth: To ostatnie zle na pewno, zaraz poprawie te czesc.

Nadia: Mamy wstep do analizy matematycznej , algebre i Matematyke 1

Garth: Mielismy napisac zaprzeczenie tej implikacji. ¬(p ⇒ q) ⇔ ¬(¬p ∨ q) ⇔ p ∧ ¬q Wykorzystalem wspomniane wczesniej prawo eliminacji implikacji a nastepnie prawo de Morgana. Mamy zdanie: (|x| < 1 ⇒ x² − x < 0) A wiec jego zaprzeczeniem [czyli ¬(p ⇒ q)] bedzie: (|x| < 1 ∧ x² − x ≥ 0)

Nadia: A to ostatnie zadanie źle zapisane?

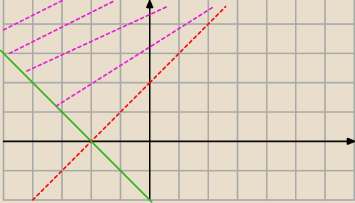
Garth: Mamy tam nie okrag, ale kolo, wspolrzedne i promien dobrze. Drugie tak [o ile sie nie myle]: x + 2 < y ∧ x + 2 ≥ −y y > x + 2 ∧ y ≥ −x − 2 A wiec szukamy czesc wspolna tych plaszczyzn. A takze wracajac, czesc wspolna tych plaszczyzn z naszym kolem.

Nadia: ok dziękuje bardzo za pomoc.

Garth: Jeszcze tam mielismy okreslic wartosc logiczna tego zaprzeczenia, ale nie bardzo wiem, jak sie za to zabrac, byly tam jeszcze jakies zalozenia?

Nadia: Oj jeszcze znalazłam 1 rzecz x≥|y| ⇒ x≤2 Jak takie cudo zapisać graficznie ?

Nadia: Rzeczywiste

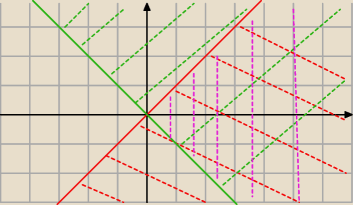
Garth: |y| ≤ x y ≤ x ∧ y ≥ −x Czesc wspolna powyzszych powierzchni