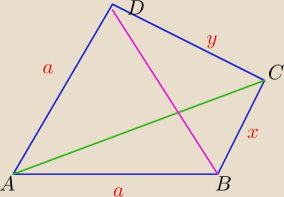
Sprawdzenie Piotr 10: W okrąg o promieniu 1 wpisano czworokąt ABCD, w którym IABI=IADI. Miara kąta BCD równa jest 120⁰, a stosunek pól trójkątów ABC i ACD wynosi 1:2. Oblicz obwód i pole tego czworokąta. Wyszło mi tak: I<DABI=60⁰; Δ ADB jest równoboczny. a=√3 2x=y

	3		6
x=		czyli y=
	7		7

	9
Ob=2√3+
	7

P_czworokąta=P_ΔDAB+P_ΔDCB

	3√3
PΔDAB=
	4

	1		3		6		18		9
PΔDCB=		*		*		*sin1200=		=
	2		7		7		196		98

	3√3		9
Pczworokąta=(		+		) j2
	4		98

Bardzo proszę o sprawdzenie

wredulus_pospolitus: a w jaki sposób wyliczyłeś 'a' ?

Piotr 10: Można w dwa sposoby: Twierdzenie sinusów:

a
	=2*R
sinα

a=√3 lub

a2√3		a3
	=
4		4*R

wredulus_pospolitus: to oczywiste jest skąd ... ale nie napisałeś a proporcja 2x=y skąd masz ?

Piotr 10: Z przyrównania pól:

	√3*IACI*x
PΔABC=
	4*R

	√3*IACI*y
PΔACD=
	4*R

Wiem, że: 2*P_ΔABC=P_ΔACD I z tego otrzymałem 2x=y

Piotr 10: I jak ?

retry92: Piotrze, pomógłbyś tu ? https://matematykaszkolna.pl/forum/217785.html Ostatnio fajnie mi wytlumaczyles a nie radze sobie z ta trygonometria..

Piotr 10: Sprawdzi ktoś

Godzio: Wygląda ok

wredulus_pospolitus: hmmm tw. cosinusów stosujemy:

	1
3 = 4x2 + x2 + 2*2x2*		=> 3 = 7x2 ... okey
	2

no to wygląda dobrze dalej jest okey jak dla mnie

Piotr 10: Dzięki