Nierówności Niko: Czy moglibyście pomóc mi rozwiązać taką nierówność 8^x+5*2^x≥2+4^x+1 Doprowadziłem to do tej postaci: 2^3x+5*2^x≥2+2^2x*2² ale nie wiem co dalej.

Aga1.: Podstaw pomocniczą zmienną t=2^x i t>0 t³+5t≥2+4t²

Niko: tylko szczerze mowiąć nie wiem co zrobić jeśli mam t³...

Niko: Czy x=1 ?

daras: przenieś wszystko na lewą str. i poszukaj pierwiastków tw. Bezouta: https://matematykaszkolna.pl/strona/120.html

Niko: czyli rozumiem że xnie jest równe 1 tak? Tw. Bezouta nie znam i nie potrafie tego zrobić

Antek: Jesli nie znasz tego twierdzenia to wroc do wielomianow i poznaj je . Dopiero potenm bierz sie za nierownosci i rownania wykladnicze

Niko: czytam milion razy to twierdzenie na tej stronie i i tak nie rozumiem o co w nim chodzi

Niko: Pierwiastek bezouta jest 2 I co dalej?

Niko: czyli t=2 a jesli tak to 2=2^x w takim razie x=1 Dobrze?

Garth: Nie ma czegos takiego jak "pierwiastek bezouta". Jest cos takiego jak pierwiastek. Jezeli znalazles pierwiastek dla swojego wielomianu, ktorym jest tutaj t³ − 4t² + 5t − 2 ≥ 0, to znajac twierdzenie Bezout wiesz, ze ten wielomian dzieli sie przez x − a, gdzie a to ten znaleziony pierwiastek [w tym przypadku, o ile na pewno 2 jest tym pierwiastkiem, to wielomian dzieli sie przez t − 2]. Nastepnie szukasz kolejnych pierwiastkow, bo moze ich byc wiecej. Po podzieleniu bedziesz mial juz nierownosc kwadratowa, wiec bedzie o wiele latwiej, bo mozna posluzyc sie wzorami na pierwiastki rownania kwadratowego.

Niko: Ok. Podzieliłem. Ostatecznie oprócz t=2 wyszło z równania kwadratowego t=1. I teraz obydwa podstawiam do t=2^x?

Garth: Tak, jesli t = 2 lub t = 1 to podstawiasz. 2^x = 2 lub 2^x = 1

daras: 2 nie jest pierwiastkiem wielomianu bo W(2)≠0

daras: 1 tez nie jest: W(1)=2≠0

daras: pierwiastek jest ułamkowy 0<t<1 http://www.jogle.pl/wykresy/

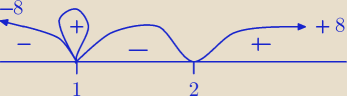
daras: @Garth masz rację t³−4t²+5t−2≥0 Rozważałem trochę inny wielomian czyli W(2)=0 i W(1)=0⇒1 i 2 sa pierwiastkami wielomianu czyli (t−1)²(t−2)≥0 teraz metodą pętelkową wyznaczamy rozwiązanie tej nierówności Spełniają ją t =1 i t ≥ 2 dalej ty..

daras: PS. podany przeze mnie wyżej link do rysowania wykresów funkcji znacznie skraca proces znajdowania pierwiastków, nazwałbym to nawet Bezoutem graficznym