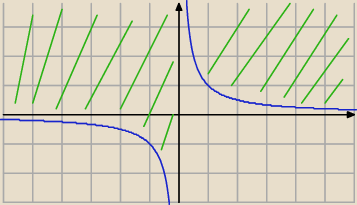
logika PuRXUTM: mam zastrzeżenia co do zadania https://matematykaszkolna.pl/forum/215547.html xy<1 ⇒ xy=1 zał: x,y≠0 możemy to przekształcić

	1		1
(xy<1 ⇒ xy=1) ⇔ ¬(xy<1) v xy=1 ⇔(xy≥1) v xy=1 ⇔ y≥		v y=		czyli wq mnie wykres
	x		x

powinien wyglądać tak ale pewnie nie jestem, moja pani od logiki niestety nie ogarnia...

Mila: Tam tyle komentarzy! Napisz to zadanie jeszcze raz. Rozwiążę. Wtedy podyskutujemy.

PuRXUTM: Mila wiem że tyle komentarzy... ale i tak nie ogarniam, po drugie na ćwiczeniach miałem inaczej... a polecenie do zadania brzmi : Znajdź wykresy funkcji zdaniowych fi(x,y), gdzie zakresem zmienności zmiennych x oraz y jest zbiór liczb rzeczywistych: c)xy<1 ⇒ xy=1 no i moje "przemyślenia" xy<1 ⇒ xy=1 zał: x,y≠0 możemy to przekształcić (xy<1 ⇒ xy=1) ⇔ ¬(xy<1) v xy=1 ⇔(xy≥1) v xy=1 ⇔

	1		1
y≥		v y=
	x		x

czyli wq mnie wykres powinien wyglądać jak wyżej...

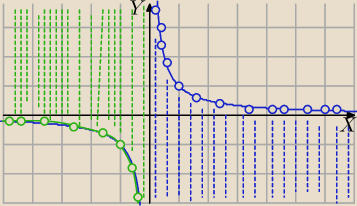
Mila: x≠0 1) x>0

	1
y<		punkty poniżej prawej gałązki wykresu
	x

2) x<0

	1
y>		punkty powyżej lewej gałązki wykresu
	x

Mila: 1) lub 2) suma zbiorów

PuRXUTM: Mila, ale dlaczego tak to już jest 3 rozwiązanie albo 4 jakie widzę Każde inne

Mila: Weź punkt z Twojego wykresu np. (2,2) z obszaru zielonego 2*2=4>1 a ma być <1 Zatem ten obszar zielony z prawej nie pasuje. weź punkt poniżej Twojego zielonego obszaru z prawej strony osi Oy (2,−3) 2*(−3)=−6<1 a Ty nie zaznaczyłes tego obszaru. Wczytaj się w moje rozwiązanie, to zrozumiesz.

Aga1.: Wydaje się,że Mila nie zauważyła implikacji i rozwiązała nierówność xy<1. (p⇒q)⇔(∼pvq) A implikacja zastąpiona alternatywą (xy≥1 v xy=1to po prostu xy≥1. Rozpatrujesz 2 przypadki 1) xy≥1 //:x i x>0 Nie zmieniasz kierunku nierówności

	1
y≥
	x

2) xy≥1 //:x i x<0

	1
y≤
	x

PuRXUTM: czytam czytam i dalej nie rozumiem dlaczego zmieniłaś nierówność i dlaczego rozważasz przypadki dla x (dlaczego nie rozważasz też dla y )

PuRXUTM: aha Aga1 bo jak dzielę obustronnie przez liczbę ujemną to się zmienia znak nierówności... dzięki ! Tobie Milu też dziękuje

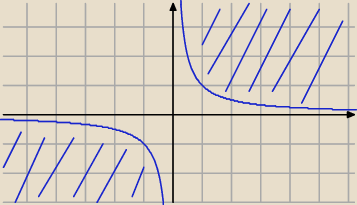
PuRXUTM: czyli wykres taki jak na ćwiczeniach

Mila: Tak , Aga ma rację. Rozwiązałam tylko nierówność. Teraz wszystko jasne? O implikacji nie pomyślałam.

PuRXUTM: jasne jak słońce dzięki wielkie Jak możesz to pomóż przy kolejnych zadaniach

Mila: No, może tym razem wszystko zauważę, albo bedzie dyskusja.

PuRXUTM: Milu nawet lepiej jak nie zauważysz, bo wtedy bardziej dogłębnie przeanalizuje problem kolejne zadanie już wrzuciłem podbije je