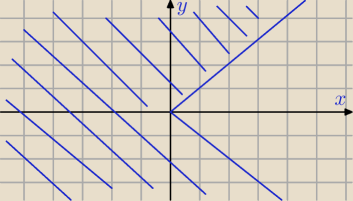
logika (podobno :) ) PuRXUTM: mam narysować wykres x<|y| czyli mogę sobie to rozpisać y>x v y<−x

PuRXUTM: od razu kolejny do tego podpunkt narysować wykres xy<1 ⇒ xy=1 w tym to nie mam pojęcia jak to zrobić...

PuRXUTM: dokładne polecenie to znajdź wykres funkcji zdaniowych α(x,y), gdzie zakresem zmienności zmiennych x oraz y jest zbiór liczb rzeczywistych

PuRXUTM: c) ax+by+c=0 a,b,c∊R − to będą wszystkie proste w układzie współrzędnych

pigor: ..., xy< 1 ⇔ y< ¹_x i x≠0 (przerywaną linią hiperbola y= ¹_x, czyli punkty poniżej niej bez punktów asymptoty x=1 − przerywana linia . ...

pigor: ..., ax+by+c=0 a,b,c∊R ja bym powiedział po prostu (x,y)∊RxR= R² − płaszczyzna .

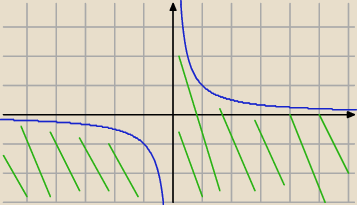
PuRXUTM: dlaczego bez x=1 ? ma to jakiś związek z xy=1

pigor: ..., x< |y| ⇔ |y| >x ⇔ (y< −x ∨ y >x) ∧ x >0 ⇔ (y< −x ∧ x >0) ∨ (y >x ∧ x >0) a więc osie liczbowe i proste y= ±x − przerywana linia , a szukane punkty to suma punktów (obszar) w I−ej ćwiartce nad prostą y=x , oraz pod y= −x w IV−tej ćwiartce .

pigor: ... ma z tym związek, ale taki, że masz nierówność mocną < , a nie ≤ słabą , więc oś OY przerywaną linią najlepiej . ...

PuRXUTM: przeraża mnie ta matma, wyobrażałem to sobie inaczej, myślałem że będzie ciężko, ale nie przypuszczałem że prawie żadne zadanie nie będę umiał zrobić...

PuRXUTM: dlaczego (y< −x ∨ y >x) ∧ x >0

pigor: ... , cóż, mogę cię tylko pocieszyć , że nie jesteś w tym osamotniony zapewne i zadajesz sobie pytanie, dlaczego to już dobrze, a będzie na pewno dobrze jak sam sobie na nie odpowiesz; pozdrawiam i życzę trafnych wyborów, aby temu zaradzić i powalczyć.

diego: |y|>x⇔ y>x dla y>=0 y<−x dla y<0

pigor: ... no bo tylko wtedy mam tę alternatywę koniunkcji, ale dzięki temu pytaniu przypomniałeś mi (dziękuję, a więc z Tobą nie jest tak źle − wszystko da się pokonać ), że opuściłem druga możliwość − kurcze − mianowicie ∨ (x< 0 i y∊R) , a więc zamaluj jeszcze całą stronę lewą płaszczyzny układu XOY bez punktów półosi OX (tylko punkty wewnątrz ćwiartki II i III) . ...

PuRXUTM: pigor dziękuje za zadania i odpowiedź możesz mi jeszcze tu coś potłumaczyć dlaczego x>0

pigor: ... zauważ jeszcze, że punkt (0,0) także nie spełnia danej nierówności 0<0, dlatego nigdzie nie ma u mnie znaków ≤ (≥)

PuRXUTM: właśnie na analizie gościu powiedział że 0<0 i 0>0 ale to chodziło o to że jak jest funkcja rosnąca i stała to jest rosnąca

diego: 0 nie jest większe od 0. Nie wiem kto ci to podał, ale to nie jest prawda

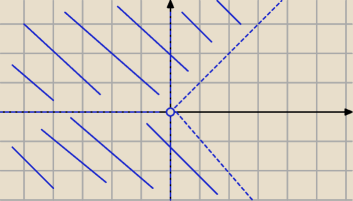
PuRXUTM: osie przerywane

PuRXUTM: @diego jakiś doktor więc ma rację A Ty gdzie się uczysz

diego: To że ma doktorat to nie znaczy że się nie myli. Czyli analogicznie wg niego 1>1? bzdura totalna.

PuRXUTM: chodzisz do LO

pigor: .., no bo to "szkolna" nierówność , ale niestety 99% uczniów nie zwraca na założenia, definicji, określeń, twierdzeń, wręcz przeciwnie − jak słyszę − co niektórzy kłócą się o zaniżenie oceny, jeśli znak nie taki jaki powinien być itp. itd , a więc dlatego, że |x| >a i a>0 ⇔ x< −a lub x>a, natomiast |x| >a i a<0 ⇔ x∊R\{0} i to tyle teraz tylko trzeba się z tym ... "przespać" i wtedy się albo zrozumie , albo zapomni, przy czym jeśli to drugie, a komuś zależy na tym, aby ... , musi się znowu z tym ... przespać itd, itp., aż w końcu ... jakie to proste i oczywiste hurraaa .

diego: A dlaczego o to pytasz? Uważasz że jestem zbyt "głupi" żeby wiedzieć że 2+2=4?

PuRXUTM: nie diego, wręcz przeciwnie tylko że to są studia, nie zrozumiesz dopóki nie zobaczysz np w szkole uczą że nie ma czegoś takiego jak √−1 a na studiach jest i odziwo jest to bardzo przydatne ostatnio na wykładzie miałem że 1+1=0 ale to pod pewnymi założeniami

PuRXUTM: pigor dzięki wielkie za pomoc ! Bo bez Was (pomagaczy ) było by 3x gorzej...

diego: Właśnie z pewnymi założeniami. Bez nich ten zapis nie ma sensu. Na twoje poprzednie pytanie odpowiem tylko w ten sposób − moich studentów nikt nie uczy, że w zbiorze liczb rzeczywistych 0>0

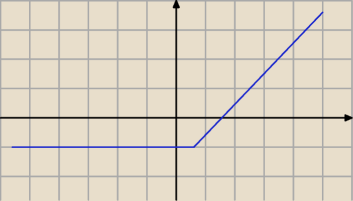
PuRXUTM: aha czyli jesteś wykładowcą, no to powiem tak jeśli mamy taką funkcję (jak na rysunku) to na studiach jest ona rosnąca prawda czyli x1<x2 ⇒ f(x1)<f(x2) czyli jeśli −2<−1 to −1<−1 o to mu chodziło

PuRXUTM: ej diego okłamałeś mnie... takie zadania dodajesz, na pewno nie masz swoich studentów, no chyba że kolegów

diego: Ta funkcja nie jest ściśle monotoniczna − jest to funkcja niemalejąca − stała bądź rosnąca. Wobec tego wg mnie powinna być nierówność nieostra. Ogólnie wprowadza się następujące pojęcia: funkcja rosnąca, ściśle rosnąca (malejąca) − nierówność ostra. funkcja niemalejąca (słabo rosnąca) − nierówność słaba. funkcja nierosnąca (słabo malejąca) − nierówność słaba.

diego: Mam wiele nicków. Nie ulegaj złudzeniom

Michał: A zmiana nicku to chwila.

Trivial: PuRXUTM, pierwiastek z √−1 nie istnieje przy rozważaniu tylko liczb rzeczywistych. Liczby zespolone zostały zdefiniowane tak, aby pierwiastek ten istniał i liczby te były zamknięte ze względu na pierwiastkowanie. Dzięki temu każdy wielomian zespolony stopnia n ma dokładnie n pierwiastków z uwzględnieniem krotności. Pamiętaj, że coś nie istnieje dopóki nie zostanie stworzone.

PuRXUTM: diego nie mąć proszę

PuRXUTM: witaj Trivial

Trivial: Witaj.

PuRXUTM: umrę przy tej matmie...

Garth: Nie tylko Ty.

Trivial: Nikt nie kazał Wam studiować matematyki. Można wybrać coś bardziej "uziemionego".

PuRXUTM: wiem że nikt nie kazał ale myślałem że będzie to inaczej wyglądało...

Garth: Bynajmniej nie chodzi o to, ze matematyka sie nie podoba...tylko to chyba my sie matematyce nie podobamy.

PuRXUTM: hahha

Trivial: PuRXUTM, no to możesz winić tylko siebie. W dobie internetu można takie rzeczy wyszukać w kilka minut.

Trivial: http://www.matematyka.pl/309003.htm

matyk: Pomyślcie co mieli studenci 20 lat temu − internetu brak. Tylko w bibliotekach siedzieli...

Trivial: Hmm.. Pewnie zamiast maili wysyłali sobie listy z załącznikami.

Garth: Priorytetem.