Problem z parametrem. Wojtuś: Mam mały problem z zadaniem: W zależności od parametru p ∊ R rozwiąż (1−p)(|x+2|+|x)|=4−3p Na początku podzieliłem aby po lewej stronie zostało samo x

	4−3p
|x+2|+|x|=
	1−p

wyznaczyłem dziedziny x 1* x∊(− nieskończoność , −2 ) 2* x∊<−2, 0 ) 3* x∊<0, + nieskończoność ) Wiem też, że po prawej stronie jest funkcja homograficzna z parametrem p o wzorze f(x)=

	4−3p
		i wiem jak ją narysować. Asymptoty są w punktach x=1 oraz y=3
	1−p

Tylko teraz nie wiem jak połączyć równania x z równaniem homograficznym tak żeby wyznaczyć ilość rozwiązań. Dlatego proszę o w miarę szybką podpowiedź. P.S jest to zadanie konkursowe dlatego nie chcę całego rozwiązania tylko ewentualnego nakierowania mnie na rozwiązanie i ewentualne podanie wyników, tak żebym znając metodę mógł sam dochodzić do odpowiednich rozwiązań Dziękuję, czekam na wskazówki

Piotr 10: Troszkę utrudniasz sobie zadanie

...-:):

	4−3p
...		... nie jest f(x)
	1−p

Wojtuś: To jak proponujesz ? Wpadłem tylko na pomysł narysowania funkcji homograficznej z prawej strony, bo nie wiedziałem jak dalej to ruszyć

Piotr 10: Moment muszę rodzicom pomoć

Piotr 10: Rozważ na początku, co się będzie działo gdy 1−p=0 oraz 4−3p=0

Wojtuś: Ok, poczekam

	4−3p
...− skoro		nie jest f(x) to nie mogę przyrównać tego do tej funkcji.
	1−p

To teraz całkiem nie wiem jak ruszyć.

...-:):

	4−3p
...		<2
	1−p

=2 >2

Wojtuś: tak już to rozważyłem, tylko właśnie nie wiem czy teraz zrobić przedziały do których p należy i odwoływać się do przedziałów x ?

Piotr 10:

	4
Jeśli to rozważyłeś, to co z tego wynika, jeśli p=1 oraz p=		?
	3

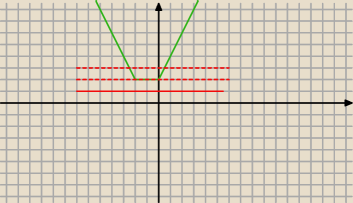
...-:): ... rozważ |x+2|+|x|=m i ilość rozwiązań w zależności od m

	4−3p
a potem przyrównaj do
	1−p

...-:): ... tu masz podobne https://matematykaszkolna.pl/forum/215581.html

Wojtuś:

	4
No to jeżeli p =		to albo |x+2|+|x|=0 albo 1−p=0 ale |x+2|+|x| ≥ 2 więc nie może być
	3

	4
zerem a 1−p też nie może być równe zero po p =		o ile dobrze myślę, więc dla p = U{4}{3
	3

i p=1 brak rozwiązań.

Piotr 10:

	4
No właśnie dla tych wartości, czyli dla p=		oraz p=1 brak rozwiązań, czyli jaki to układ?
	3

Piotr 10: Dla p=4/3 mamy:

	4
(1−4/3)*(|x+2|+|x)|=4−3*
	3

Ix+2I+IxI=0 brak rozwiązań dla p=1 (1−1)(|x+2|+|x)|=4−3*1 0≠1

Wojtuś: Czyli teraz wyznaczyć przedziały p ? czyli:

	4
p∊(−∞,		)
	3

	4
p∊(		, 1)
	3

p∊ (1, +∞) I na podstawie tych przedziałów wyznaczyć x ?

Piotr 10:

	4−3p
Teraz masz Ix+2I+IxI=		i kiedy to będzie miało rozwiązanie ? Czyli będzie układ
	1−p

oznaczony ?

Wojtuś: Układ oznaczony wtedy jak jest jedno rozwiązanie. wydaje mi się że ten układ będzie miał rozwiązania w zależności od p czyli od przedziałów, które wyżej wyznaczyłem tak ? I wtedy będę mógł określić wartość wyrażenia po prawej stronie i do tego dopasować ilość rozwiązań x tak ?

Piotr 10:

4−3p
	> 0
1−p

Rozwiązałeś tak?

Saizou : nie mam nic przeciwko pomaganiu Piotrze10 ,ale to tak trochę nie halo, bo to zadanie konkursowe

Piotr 10: Sam musisz sobie poradzić dalej, ja już za dużo Ci podpowiedziałem. Zmykam

Piotr 10: Tak wiem Saizou za bardzo chciałem pomóc

Saizou : jak dla mnie jest to trochę nie fair wobec innych, którzy sami bez żadnych podpowiedzi walczą z zdaniami

Wojtuś: Dziękuję bardzo za pomoc, po prostu nakierowałeś mnie na rozwiązanie Przeanalizuję wskazówki i pochwalę się rozwiązaniem jak minie termin składania prac Jeszcze raz WIELKIE dzięki

Wojtuś: Na te zadania jest miesiąc wcześniej czasu i jest powiedziane, że można konsultować się z nauczycielami podczas robienia tych zadań. A moja nauczycielka matematyki sama nie potrafi wytłumaczyć najprostszych rzeczy bez podręcznika to takie zadania tym bardziej. Dlatego szukam w internecie pomocy

Piotr 10: