nierównośż z wartością bezwzględną mata: pomóżcie l−x−2xl≤2−x

wredulus_pospolitus: |−x−2x| = |−3x| i rozdziel na dwa przypadki

mata: chyba nie rozumiem

Bogdan: |−3x| = |3x| = 3|x| Dwa przypadki: dla x< 0, dla x≥0:

HELP: zgubiłam− powinno być l−x²−2xl≤2−x

Antek: https://matematykaszkolna.pl/strona/2545.html zobacz jak tam zamieszcone przyklady sa rozwiazane .

HELP: nie rozumiem tego

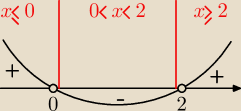
Bogdan: |−x² − 2x| = |−x(x + 2)| = |x(x + 2)|, x₁ = 0, x₂ = 2 Rozpatrujemy 3 przypadki: 1) dla x≤0: x² + 2x ≤ 2 − x 2) dla x∊(0, 2): −x² − 2x ≤ 2 − x 3) dla x≥2: x² + 2x ≤ 2 − x

pigor: ... rozwiąż nierówność l−x²−2xl ≤2−x . −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− bardzo ładnie rozwiązuje sie z pomocą wykresów L−ewej i P−rawej strony; , a ponieważ przecinają się w x=1 i x=2 łatwo odczytać, że wykres L−ewej strony ≤ , czyli poniżej lub na wykresie) P−rawej ⇔ −1≤ x ≤1, a więc przedział x∊[−1;1 jest rozwiązaniem danej nierówności. ...

HELP:

	−3−√17		−3+√17
mnie wyszło zupełnie coś innego		i
	2		2

dlaczego?

HELP: dlaczego?

pigor: ...no tak , przepraszam, masz rację; ja niestety rysowałem nie to równanie, bo rysowałem sobie parabolę y= x²−2x zamiast y=x²+2x ; przepraszam jeszcze raz, −−−−−−−−−−−−−−−−−−− a rozwiązanie analityczne, mogłoby wyglądać np. tak : l−x²−2xl ≤ 2−x ⇔ |x²+2x| ≤ 2−x i 2−x ≥0 ⇔ x−2 ≤ x²+2x ≤ 2−x i x ≤ 2 ⇒ ⇒ x²+x+2 ≥0 i x²+3x−2≤ 0 ⇔ x∊R i −¹₂(3+√17)≤ x ≤ ¹₂(−3+√17< 2 ⇔ ⇔ x∊<−¹₂(3+√17) ; ¹₂(−3+√17>