wektory
zadanie: dane sa trzy wierzcholki rownolegloboku ABCD: A(0,0), B(3,1), D(−1,1). wyznacz wspolrzedne
wierzcholka C.
C(x,y)
wektor AD=[−1,1]
wektor BC=[x−3, y−1]
wektory AD i BC sa rowne bo maja takie same kierunki, zwroty i dlugosci (dlugosci bo sa to boki
rownolegloboku odpowiednie te na przeciwko)
czyli AD=BC
[−1,1]=[x−3, y−1]
C(2,2)
ale rowniez AD=CB
czyli drugi punkt C(4,0)
dwa punkty wyszly mi z rysunku ze moga byc
dobrze?
jezeli nie to prosze o wyjasnienie bledow
10 paź 18:57
zadanie: ?
10 paź 20:05
zadanie: ?
10 paź 20:35
krystek: AD→≠CB→
10 paź 20:42
krystek:
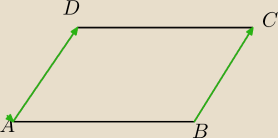
10 paź 20:45
zadanie: czyli tylko punkt C(2,2) jest dobrze?
10 paź 20:47
krystek: tak
10 paź 20:55
zadanie: dziekuje
10 paź 20:58
zadanie: mam jeszcze pytanie
jak odroznic na rysunku czy dany wektor jest suma czy roznica mi sie to myli
na co zwracac uwage?
10 paź 21:00
10 paź 21:01
10 paź 21:02
zadanie: wiem patrzylem na to
a na przyklad skad mam wiedziec jaka droge pokonac od jakiegos punktu do drugiego za pomoca
wektorow?
10 paź 21:09
Mila:
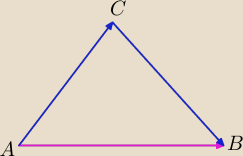
Z punktu A do punktu B możesz iść różową drogą albo niebieską
AB
→=AC
→+CB
→
10 paź 21:59
Mila:
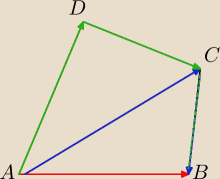
AB
→=AC
→+CB
→
AB
→=AD
→+DC
→+CB
→
10 paź 22:20
zadanie: dziekuje
11 paź 08:11
zadanie: zawsze sie boje, ze sie pomyle z tymi odcinkami a mianowicie z dodawaniem i z odejmowaniem
dlatego prosilbym o jakies zadanie jak dojsc do jakiegos punktu na kilka sposobow z
odejmowaniem oraz z dodawaniem tych wektorow
11 paź 19:15
zadanie: Dla jakich x wektory [x,x
2] i [−3,9] sa liniowo zalezne czyli rownolegle?
t∊R
t[x,x
2]=[−3,9]
tx=−3
tx
2=9
stad
9t=9t
2
9t
2−9t=0
9t(t−1)=0
t=0 lub t=1
czyli x=−3 i x=0 ale wtedu w mianowniku bedzie t=0 ?
11 paź 20:15
zadanie: ?
11 paź 21:32
Basia:
dla x=0 dostajesz wektor [0;0] czyli wektor zerowy, który jest równoległy do każdego innego
wektora
a więc także do wektora [−3;9]]
i są to wektory liniowo zależne; ponieważ
0*[−3;9]] = [0;0] = [x;x2]
nie byłoby tego problemu, gdybyś zrobił odwrotnie
−3t = x
9t = x2
9t = (−3t)2
9t = 9t2
9t2 − 9t = 0
9t(t−1) = 0
t= 0 lub t=1
x=0 lub x = −3
czyli szukany wektor to [0;0] lub [−3;9]]
innych nie ma
11 paź 22:30
zadanie: dziekuje
11 paź 22:36
zadanie: jeszcze prosilbym o to zadanie co napisalem o godzinie 19:15 z tymi wektorami
niekoniecznie dzisiaj bo ja juz ide spac
11 paź 22:40
Mila:
Dziękuję Basiu, tak myślałam, ale trochę mi to zardzewiało w mózgu i wolałam Twoje
rozwiązanie.
Zadanie 1 − WEKTORY
Dany jest prostokąt ABCD. Wektor AB→=3p→, zaś AD→=4q→.
Wyznaczyć wektory : AM→, AN→ MN→
w zależności od wektorów p i q, wiedząc, że M i N są odpowiednio środkami boków CD i BC.
Czekam na Twoje rozwiązanie. Następne zadanie będzie trudniejsze.
11 paź 22:40
zadanie: dziekuje ale jutro je zrobie bo juz nie mam sily
11 paź 22:43
Mila:
Dobranoc, dobrych fluidów życzę.

11 paź 22:45
zadanie: jest to prostokat wiec
wektor AD=BC=4q
AB=DC=3p
| | 1 | |
AM=AD+DM=4q+ |
| *3p=3p+2q+4q |
| | 2 | |
AN=AB+BN=3p+2q
MN=AN−AM=3p+2q−
12 paź 16:01
zadanie: jeszcze nie dokonczylem
12 paź 16:01
zadanie: | | 1 | | 1 | |
MN=AN−AM=3p+2q−4q− |
| *3p= |
| *3p−2q |
| | 2 | | 2 | |
12 paź 16:03
zadanie: | | 1 | |
tam powinno byc tylko AM=AD+DM=4q+ |
| *3p |
| | 2 | |
12 paź 16:05
zadanie: dobrze?
12 paź 16:05
zadanie: mam 2 zadania, z ktorymi mam problem
1. .Dane sa wspolrzedne punktow P Q R bedacych srodkami bokow trojkata ABC.Znajdz wspolrzedne
punktow A B C.Rachunki warto przeprowadzic na wektorach wodzacych a nie we
wspolrzednych.Dlaczego?
2. Uzasadnij poslugujac sie wspolrzednymi i wektorami, ze w trapezie o podstawach a i b
przekatne przecinaja sie w stosunku a:b.
12 paź 16:08
zadanie: prosilbym o pomoc w ich rozwiazaniu
12 paź 16:09
Mila:
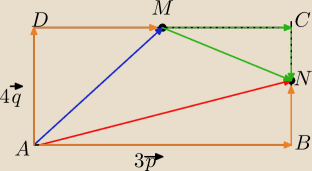
Były tam literówki u Ciebie, napisałam z rysunkiem.
1)
| | 1 | | 3 | |
AM→=4q→+ |
| *3p→= |
| p→+4q→ |
| | 2 | | 2 | |
| | 1 | |
2) AN→=3p→+ |
| *4q→=3p→+2q→ |
| | 2 | |
| | 1 | | 1 | | 3 | |
3) MN→= |
| AB→+ |
| *(−4q→)= |
| p→−2q→ |
| | 2 | | 2 | | 2 | |
12 paź 16:24
zadanie: dobrze, dziekuje
12 paź 16:27
Mila:
Wiadomości:
a
→+b
→+ c
→=0
Z trzech wektorów, z których każde dwa są nierównoległe można zbudować trójkąt, jeżeli ich
suma jest równa zero.
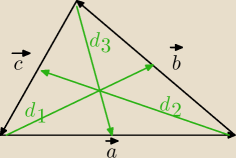
Zadanie2.
Wektory a
→, b
→, c
→ są bokami trójkąta . Wyznaczyć środkowe tego trójkąta w zależności od
wektorów a
→, b
→, c
→.
Zadanie3.
Wykazać, że ze środkowych można zbudować trójkąt.
12 paź 16:43
zadanie: 2.
3.
d
1+d
2+d
3=0
| | b | | c | | a | |
c− |
| +a− |
| +b− |
| =0 /*2 |
| | 2 | | 2 | | 2 | |
a+b+c=0 czyli mozna zbudowac trojkat
dobrze?
12 paź 18:00
zadanie: ?
12 paź 19:30
zadanie: zalamala sie pani tym rozwiazaniem, ze nic nie pisze ?
12 paź 20:36
Mila: Nie, komputer włączony, ja gdzieś biegam. Już sprawdzam.
12 paź 20:48
Mila:
POpraw . Patrz jak dojść do punktu w którym jest grot środkowej,każdą środkową przedstaw na dwa
sposoby.
3) dobrze, z fałszu wyniknęła prawda.
12 paź 21:00
Piotr 10:
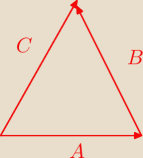
Przepraszam za wejście. Miałem ostatnio problemy z wektorami, i czy
Mila nie powinno być
tak post 16:43 ?
12 paź 21:04
Mila:
Możesz tak oznaczyć: zależy do czego to jest potrzebne.
U Ciebie jest :
A→+B→=C→ w takim razie :
A→+B→−C→=0
12 paź 21:14
Piotr 10: A ok, dzięki

. Pozdrawiam

12 paź 21:17
13 paź 15:45
Mila:
| | a | | a | |
d3=c+ |
| lub d3= −b− |
| |
| | 2 | | 2 | |
13 paź 18:01
zadanie: tylko 2 dobrze mialem
dziekuje
13 paź 18:22
zadanie: moglbym prosic o jakies podpowiedzi do zadan z 16:08 ?
13 paź 18:24
Mila:
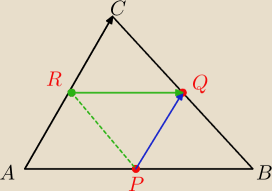
P=(p1,p2)
Q=(q1,q2)
R=(r1,r2)
(odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i równy jego
połowie )
PQ
→=[q1−p1,q2−p2]
C=(r1+q1−p1,r2+q2−p2) wsp. punktu po translacji R o wektor PQ
→
(do wsp. punktu R dodajemy współrzędne wektora)
A=(r1−(q1−p1),r2−(q2−p2))wsp. punktu po translacji R o wektor (−PQ
→)
Pozostaje wyznaczyć wsp. B Zrób to sam.
Nie wiem, czy o to chodziło.
Znajdę konkretne zadanie, to napiszę.
13 paź 18:54
Mila:
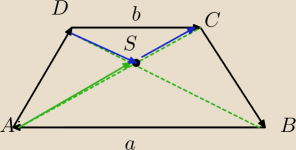
Uzasadnij poslugujac sie wspolrzednymi i wektorami, ze w trapezie o podstawach a i b
przekątne przecinaja sie w stosunku a:b.
AB||DC
| | |AB| | | a | |
AB→=k*DC→ gdzie k= |
| = |
| |
| | |DC| | | b | |
AS
→||SC
→ i DS
→||SB
→⇔
DS
→=m*SB
→i SC
→n*AS
→ n,m∊R
z drugiej strony wiemy, że
AS
→+SB
→=AB
→
| | b | | b | |
DS→= |
| SB→ i SC→ |
| *AS→⇔ |
| | a | | a | |
Punkt S dzieli przekątne w stosunku b:a licząc od górnej podstawy natomiast w stosunku a:b
licząc od dolnej podstawy oznaczonej literą a.
13 paź 19:39
zadanie: dziekuje
14 paź 15:03

 Z punktu A do punktu B możesz iść różową drogą albo niebieską
AB→=AC→+CB→
Z punktu A do punktu B możesz iść różową drogą albo niebieską
AB→=AC→+CB→
 AB→=AC→+CB→
AB→=AD→+DC→+CB→
AB→=AC→+CB→
AB→=AD→+DC→+CB→

 Były tam literówki u Ciebie, napisałam z rysunkiem.
1)
Były tam literówki u Ciebie, napisałam z rysunkiem.
1)
 Wiadomości:
a →+b→+ c→=0
Z trzech wektorów, z których każde dwa są nierównoległe można zbudować trójkąt, jeżeli ich
suma jest równa zero.
Zadanie2.
Wektory a →, b→, c→ są bokami trójkąta . Wyznaczyć środkowe tego trójkąta w zależności od
wektorów a →, b→, c→.
Zadanie3.
Wykazać, że ze środkowych można zbudować trójkąt.
Wiadomości:
a →+b→+ c→=0
Z trzech wektorów, z których każde dwa są nierównoległe można zbudować trójkąt, jeżeli ich
suma jest równa zero.
Zadanie2.
Wektory a →, b→, c→ są bokami trójkąta . Wyznaczyć środkowe tego trójkąta w zależności od
wektorów a →, b→, c→.
Zadanie3.
Wykazać, że ze środkowych można zbudować trójkąt.
 Przepraszam za wejście. Miałem ostatnio problemy z wektorami, i czy Mila nie powinno być
tak post 16:43 ?
Przepraszam za wejście. Miałem ostatnio problemy z wektorami, i czy Mila nie powinno być
tak post 16:43 ?
 . Pozdrawiam
. Pozdrawiam 
 P=(p1,p2)
Q=(q1,q2)
R=(r1,r2)
P=(p1,p2)
Q=(q1,q2)
R=(r1,r2)
 Uzasadnij poslugujac sie wspolrzednymi i wektorami, ze w trapezie o podstawach a i b
przekątne przecinaja sie w stosunku a:b.
AB||DC
Uzasadnij poslugujac sie wspolrzednymi i wektorami, ze w trapezie o podstawach a i b
przekątne przecinaja sie w stosunku a:b.
AB||DC