układy równan
Madzik: Rozwiaz układ:
y=|x+1|
x2+y2=4y−2x+5
7 paź 21:38
7 paź 21:39
Madzik: no tak tylko tam jest zle przepisane, nie wiem co zrobić z 4y, po podstawieniu
7 paź 21:40
PW:
(1) y=|x+1|
(2) x2+2x+1+y2=4y+6
Jeżeli istnieje para (x,y) spełniająca ten układ, to z (1) wynika, że
y2=|x+1|2
(3) y2=x2+2x+1
Po podstawieniu (3) do (2) otrzymamy
y2+y2=4y+6
y2−2y−3=0
y1=−1, y2=3,
co podstawione do (1) daje
−1=|x+1| (nie ma takich liczb) lub 3=|x+1|, to znaczy x=2 lub x=−4
Rozwiązanie rozpoczęło się od zdania "jeżeli istnieje para (x,y) spełniająca ten układ, to
...". Podnoszenie do kwadratu nie było operacją równoważną (nic nie wiemy o znaku y). Należy
więc − jako niezbędny element rozwiązania − sprawdzić, czy otrzymane pary (2,3) i (−4,3)
spełniają układ równań. Dopiero po sprawdzeniu można napisać
Odpowiedź: Równanie jest spełnione przez pary (2,3) i (−4,3).
7 paź 23:28
PW: Można było też trochę inaczej − na wstępie zauważyć, że z (1) wynika y≥0 i po wyliczeniu y1=−1
od razu odrzucić ten wynik jako nie spełniający założenia.
7 paź 23:33
Eta:
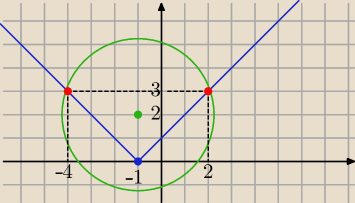 (−4,3) , (2,3)
(−4,3) , (2,3)
7 paź 23:34
Eta:
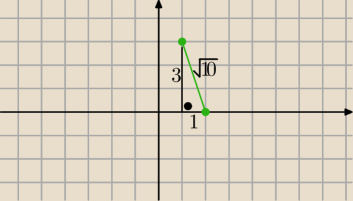
S(−1,2) , r=
√10
7 paź 23:39
Madzik: nie rozumiem co tu zostało zrobione
x2+2x+1+y2=4y+6
8 paź 00:01
Eta:
y2=(x+1)2
x2+y2=4y −2x −1+6
x2+2x+1+y2= 4y+6
(x+1)2 + y2=4y+6
y2 + y2= 4y+6
2y2−4y−6=0 /:2
y2−2y−3=0 jak nie wiesz ? to licz deltę i y1 =... y2=...
8 paź 00:07
PW: Mając pewne doświadczenie przygotowałem tak równanie (2) − dodając po obu stronach 1 i
przenosząc 2x na lewą − żeby można było podstawić to co otrzymam z (1) po podniesieniu do
kwadratu. W ten sposób zostały tylko igreki.
8 paź 00:09
PW: O, właśnie
Eta pokazała, że można było to zrobić później

8 paź 00:11
Madzik: Okej, rozumiem, dziękuje!

8 paź 00:17
Eta:
No i o to chodzi

8 paź 00:18
 (−4,3) , (2,3)
(−4,3) , (2,3)
 S(−1,2) , r= √10
S(−1,2) , r= √10


