układy równań
Madzik: rozwiaz układ rownan:
y=|x+1|
x2+y2=4x−2x+5
To tak: x2 i y2 mozna zastapic |x|2 i |y|2 ; tylko co nam to daje...prosze o pomoc...
7 paź 20:54
Piotr 10: x2+Ix+1I2=4x−2x+5
x2+(x+1)2=4x−2x+5
oraz założenie, że y≥0
7 paź 20:56
alfie: podstaw pod y w drugim rownaniu moduł |x+1| i rozwiaż rownanie kwadratowe. odrazu mowie
(x+1)2=|x+1|2 wiec moduł ci zniknie
7 paź 20:58
Madzik: tylko pomyliłam sie przy przepisywanie tam w 2 rownaniu jest
.....=4y−2x+5
to tu tez podstawiamy pod y |x+1|, tylko tu nie jest do kwadratu wiec wartosc bezwzgledna
zostanie....
7 paź 21:20
Madzik: prosze o pomoc...
7 paź 21:31
Aga1.:
A na piechotę.
Dla x≥−1 mamy układ
y=x+1
i podstawiamy do drugiego
x
2+(x+1)
2=4(x+1)−2x+5
x
2+x
2+2x+1=4x+4−2x+5
Wszystko na jedną stronę i licz x , a później y.
Gdy x<−1
to y=−x−1
i x
2+(−x−1)
2=4(−x−1)−2x+5
x
2+x
2+2x+1=−4x−4−2x+5
i licz dalej.
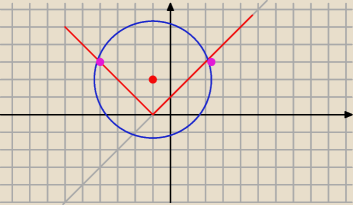
Metoda graficzna
Równanie
x
2+y
2+2x−4y−5=0 przedstawia okrąg o środku S(−1,2) i promieniu r=
√10
x=2, y=3 lub x=−4,y=3
7 paź 22:20
 A na piechotę.
Dla x≥−1 mamy układ
y=x+1
i podstawiamy do drugiego
x2+(x+1)2=4(x+1)−2x+5
x2+x2+2x+1=4x+4−2x+5
Wszystko na jedną stronę i licz x , a później y.
Gdy x<−1
to y=−x−1
i x2+(−x−1)2=4(−x−1)−2x+5
x2+x2+2x+1=−4x−4−2x+5
i licz dalej.
Metoda graficzna
Równanie
x2+y2+2x−4y−5=0 przedstawia okrąg o środku S(−1,2) i promieniu r=√10
x=2, y=3 lub x=−4,y=3
A na piechotę.
Dla x≥−1 mamy układ
y=x+1
i podstawiamy do drugiego
x2+(x+1)2=4(x+1)−2x+5
x2+x2+2x+1=4x+4−2x+5
Wszystko na jedną stronę i licz x , a później y.
Gdy x<−1
to y=−x−1
i x2+(−x−1)2=4(−x−1)−2x+5
x2+x2+2x+1=−4x−4−2x+5
i licz dalej.
Metoda graficzna
Równanie
x2+y2+2x−4y−5=0 przedstawia okrąg o środku S(−1,2) i promieniu r=√10
x=2, y=3 lub x=−4,y=3