rozwiaz nierownosc Aya: Rozwiąż nierówność |x²−x|−|x−5|<=3

Basia: masz rozwiązać algebraicznie czy wystarczy graficznie ?

Aya: algebraicznie

5-latek: https://matematykaszkolna.pl/strona/2545.html masz tutaj przyklady jak rozwiazac swoj przyklad KLikasz na niebieska strzalke i masz rozwiazanie . Sprobuj moze sama najpierw

Aya: ok.dzieki

5-latek: To moze pisz tutaj to rozwiazanie . Zawsze ktos sprawdzi

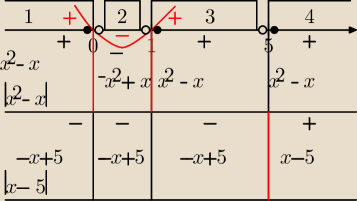
Gustlik: |x²−x|−|x−5|≤3 Metoda "osi i tabelki" Szukam miejsc zerowych modułów: x²−x=0 x(x−1)=0 x=0 v x=1 x=5 Mamy 4 przypadki: 1) (x²−x)−(−x+5)≤3 i x€(−∞, 0> 2) (−x²+x)−(−x+5)≤3 i x€(0, 1) 3) (x²−x)−(−x+5)≤3 i x€<1, 5) 4) (x²−x)−(x−5)≤3 i x€<5, +∞) Rozwiąż te 4 przypadki, wynikiem każdego przypadku bedzie częśc wspólna wyniku nierówności i założenia, a wynikiem całej nierówności − suma wyników poszczególnych przypadków.

pigor: ..., lub tak : |x²−x|−|x−5| ≤ 3 ⇔ |x²−x|≤ |x−5|+3 ⇔ −|x−5|−3 ≤ x²−x ≤ |x−5|+3 ⇔ ⇔ −|x−5|−3 ≤ x²−x i x²−x ≤ |x−5|+3 ⇔ |x−5| ≥ −x²+x−3 i |x−5| ≥ x²−x−3 ⇔ ⇔ |x−5| ≥ −(x²−x+3) i |x−5| ≥ x²−x−3 ⇔ x∊R i |x−5| ≥ x²−x−3 ⇔ ⇔ |x−5| ≥ x²−x−3 ⇔ x−5 ≤ −x²+x+3 lub x−5 ≥ x²−x−3 ⇔ x² ≤ 8 lub x²−2x+2 ≥0 ⇔ ⇔ |x| ≤ 2√2 lub x∊R ⇔ −2√2 ≤ x ≤ 2√2 ⇔ x∊[−2√2; 2√2] . ...

pigor: ..., ufff, ale się zasiedziałem; dobranoc wszystkim

5-latek: Dobranoc pigor