Jednokładność bezendu: Wyznacz współrzędne środka jednokładności w której obrazem okręgu o równaniu (x−16)²+y²=4 jest okrąg o równaniu (x−6)²+(y−4)²=16, a skala tej jednokładności jest ujemna

	16+6		0+4
S|AB|=(		,		)= (11,2)
	2		2

ok ?

bezendu: ?

Eta: ok

bezendu: A co jak jednokładność byłaby dodatnia ?

Eta: Chyba skala dodatnia

bezendu: no tak skala przepraszam

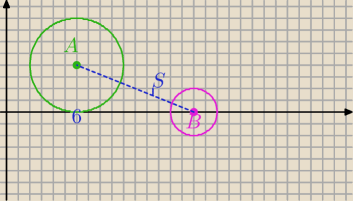
Mila: r=2 −promień mniejszego okręgu R=4− promień większego okręgu A=(6,4) B=(16,0)

	4
k=−		=−2
	2

Z definicji jednokładności: niech S=(x_s,y_s) SA^→=−2SB^→ SA^→=[6−x_s,4−y_s] SB^→=[16−x_s,0−y_s] [6−x_s,4−y_s]=−2*[16−x_s,−y_s]⇔ 6−x_s=−32+2x_s 4−y_s=2y_s

	38
xs=
	3

	4
ys=
	3

II sposób: Możesz też skorzystać z wzoru: S=(a,b) środek jednokładności, k=−2 , A=(x',y')=(6,4), B=(x,y)=(16,0) x'=k*(x−a)+a y'=k(y−b)+b

	38
6=−2*(16−a)+a⇔6=−32+2a+a⇔38=3a ⇔a=
	3

	4
4=−2*(0−b)+b⇔2b+b=4⇔b=
	3

PW: Promienie okręgów są równe 2 i 4, jednokładność przekształcająca pierwszy z nich na drugi ma więc skalę 2 lub −2, zatem w tym zadaniu skala jest równa −2. Dlaczego uważasz, że środek jednokładności leży pośrodku AB? Wtedy skala byłaby równa −1.

bezendu: PW Czyli to zadanie jest źle zrobione ?

Eta: Jasne,że źle !

bezendu: A post 21:30 ?

Eta: Podpucha

5-latek: Znasz piosenke Budki Suflera pt Nie wierz nigdy kobiEcie ? Wtedy grali bez K. Cugowskiego

bezendu: Eta

Eta: Witam "małolatka' Dla bezendu . ( robaczywka

5-latek: bezendu .Usmiechniuj sie ladnie do Ety zaraz CI sie humor poprawi

bezendu: Mila dziękuję za rozwiązanie Eta również robaczywka

Eta:

5-latek: Witam CIe Eta

5-latek: bezendu zobacz na ostatni moj wpis https://matematykaszkolna.pl/forum/211953.html

bezendu: 5−latek widziałem ( zmień kolor nick'u)