Parabola bezendu:

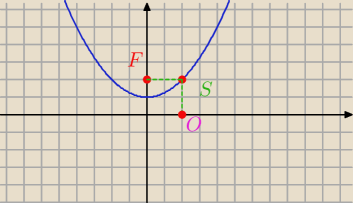
	1
Uzasadnij, że każdy punkt paraboli o równaniu y=		x2+1 jest równoodległy od osi Ox i od
	4

punktu F(0,2) |FS|=√(2−0)²+(2−2)²=2 |SO|=√(2−2)²+(0−2)²=2 ale to nie jest żaden dowód bo parabola ma nieskończenie wiele punktów więc jak zrobić to zadanie ?

Nienor: Zmienić sobie treść: Znajdź zbiór punktów(wzór), które są równoodległe od osi OX i punktu F(0,2) Może to pomoże.

Nienor: I jak idzie

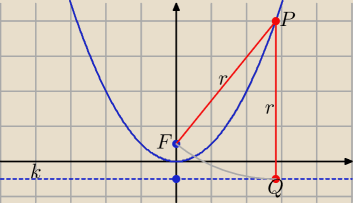
Bogdan: Kiedyś w programie nauczania geometrii analitycznej w szkole średniej były wiadomości o paraboli, hiperboli, elipsie. Podaję garść informacji (nie wszystkie) o paraboli. Definicja paraboli: Parabola jest zbiorem punktów równoodległych od prostej (zwanej kierownicą paraboli) i punktu (zwanego ogniskiem paraboli).

	1		1
y = ax2, a =		⇒ p =		, p − parametr paraboli,
	2p		2a

	1		1
p = c + d, ognisko paraboli F = (c, 0), kierownica k: = y = −d, c =		p =
	2		4a

c = d P = (x_P, y_P) − punkt na paraboli, |PQ| = |PF| = r

bezendu: Z tego warunku też nie mogę rozwiązać, myślę jeszcze nad innym sposobem

bezendu: Bogdan Mógłbyś podać mi źródło skąd masz tak ciekawe informacje ?

Nienor: Wybierasz sobie punkt P(x,y) |FP|=√x²+(y−2)² |OxP|=|y| |FP|=|OxP| √x²+(y−2)²=|y| x²+(y−2)²=y² x²+y²−4y+4=y² 4y=x²+4

	1
y=		x2+1
	4

Nienor: Bogdan to było do mnie Patrz na godzinę postów.

Bogdan: Uczyłem się tego w szkole. Informacje o krzywych stożkowych znaleźć można w każdym porządnym podręczniku do geometrii analitycznej, np. "Geometria analityczna w zadaniach" − Edward Kącki, Danuta Sadowska, Lucjan Siewierski, "Zadania z rachunku wektorowego i geometrii analitycznej" − Bogusław Gdowski, Edmund Pluciński. Myślę, że w Internecie tez można znaleźć wiele publikacji na ten temat.

bezendu: OK, dziękuje

bezendu: dziękuję*

5-latek: Np w ksiazce Matematyka dla klasy 3 piecioletniego technikum i liceum zawodowego Stefan Straszeiwcz z 1972r i ten sam autor Matematyka dla klasy 3 liceum ogolnoksztlcacego (mam ja od Krystek dla Ciebie Krysiu . jest ona z 1979r