Podanie wszystkich liczb naturalnych podzielnych przez 2,3,5 nie większych niż 5 Tomek: Podanie wszystkich liczb naturalnych podzielnych przez 2,3,5 nie większych niż 500. Wiem tylko tyle że tych liczb (naturalnych, nie większych niż 500 jest 501).

Basia: podzielnym przez 2, i przez 3, i przez 5 na pewno nie jest 501 więc napisz najpierw porządnie treść

wredulus_pospolitus: Basiu ... on dobrze napisał napisał, że liczb naturalnych nie większych niż 500 mamy 501 (sztuk) ... ale nie wie ile z nich jest podzielnych przez 2 i 3 i 5

wredulus_pospolitus: do autora: liczba podzielna ma być przez 2 i 3 i 5, czy przez 2 LUB 3 LUB 5

Tomek: Chyba lub. Wiem że rozwiązanie ma być podane w takim zapisie który składa się z 3 kół i w środku częścią wspólną jest 17 (2*3*5=30 500/30=16 z resztą + dodajemy cyfrę zero = 17) Tak nam podał wykładowca na zajęciach. I tylko tyle wiem, a jak wyliczyć resztę to nie umiem już.

wredulus_pospolitus: chyba ... to ryba

Tomek: A mógłbyś mi podać rozwiązania dla lub ?

wredulus_pospolitus: wykładowca student <szczena> to Ty bladego pojęcia nie masz o zadaniu patrząc na rozwiązanie ... mamy tutaj podzielne przez 2 i 3 i 5 a najmniejsza liczba (naturalna dodatnia) podzielna przez WSZYSTKIE te liczby to 2*3*5 = 30 <−−− taka oto więc szukasz ile liczb, które są podzielne przez 30

ICSP: najmniejsza to 0 "Naturalnych nie większych niż 500 jest 501"

Tomek: A więc 501 (o tyle mamy liczb w zbiorze?) 501/30=16 z resztą 16*30=480 tyle jest liczb w tym zbiorze podzielnych przez 2 i 3 i 5

wredulus_pospolitus: tyle znaczy ile 480 czy co

Tomek: Znaczy przepraszam. W zbiorze od 0 do 500 jest 16 liczb podzielnych i przez 2 i 3 i 5.

Tomek: Wykładowca podał że jest 17. Dlaczego?

wredulus_pospolitus: jest ich 17 0 30 60 90 120 150 180 210 240 270 300 330 360 390 420 450 480

ICSP: 0 , 30 , 60 , 90 , 120 , 150 , 180 , 210 , 240 , 270 , 300 , 330 , 360 , 390 , 420 , 450 , 480 17 liczb

Tomek: Tak samo podał że wspólnych liczb podzielnych przez 2 i 3 jest 70. 2*3=6 Przecież 501/6=83,5

Tomek: No dobra, teraz rozumiem skąd się wzięło te 17 liczb. Czyli można to obliczyć ciągiem ? Gdzie: a₁=0 a₂=30 a_n=501 r=30 Wychodzi 531=30n | :30 n=17,7 czyli 17

Garth: 501/6 = 83,5...czy rozumiesz w ogole sens tego zadania? Co to za kierunek studiujesz?

Garth: Tak, mozna ciagiem. Masz policzyc, ile jest liczb podzielnych przez 30 [czyli 0, 30, 60,... − bo te liczby przy dzieleniu przez 30 nie daja reszty] w zbiorze liczb 0, 1, 2, 3, ... , 500.

Tomek: Informatyke

ICSP: a₁ = 0 , a₂ = 30 , a_n = 501 Co to za ciąg ? Bo na pewno nie arytmetyczny.

Garth: a_n − powinien byc ostatni wyraz podzielny przez 30 z zakresu 0−500.

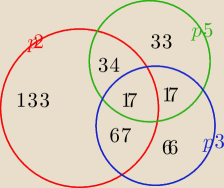
Basia: podzielne przez 2 to: 0,2,4,....,500; jest ich 251 podzielne przez 3 to 0,3,6,.....,498; jest 167 podzielne przez 5 to 0,5,10,...,500; jest ich 101 podzielne przez 2 i 3 ⇔ podzielne przez 6 to są: 0,6,12,.....,498 jest ich 84 podzielne przez 2 i 5 ⇔ podzielne przez 10 to są: 0,10,20,....,500; jest ich 51 podzielne przez 3 i 5 ⇔ podzielne przez 15 to są: 0,15,30,....,495; jest ich 34 podzielne przez 2 i 3 i 5 ⇔ podzielne przez 30 to są: 0,30,60,....,480; jest ich 17 84 − 17 = 67 51−17 = 34 34 − 17 = 17 251−34−67−17 = 251 − 118 = 133 167−67−17−17 = 100−34 = 66 101 − 34−17−17 = 101 − 68 = 33 podzielnych przez 2 lub 3 lub 5 jest: 133+33+66+34+17+67+17 policz sobie

ICSP: a₁ = 0 a₂ = 30 . . . a_n = z teorii wiesz ze a_n = a₁ + (n−1)r oraz zę r = a₂ − a₁ r = a₂ − a₁ = 30 − 0 = 30 a_n = 30n − 30 − to jest wzór ogólny twojego ciągu Teraz szukamy takiego największego n ∊ N aby była spełniona nierówność : a_n ≤ 501 ⇒ 30n − 30 ≤ 501 ⇒ 30n ≤ 531 ⇒ n ≤ 17,7 ⇒ n = 17

Tomek: Dziękuję Basiu. Teraz zachodzi pytanie. Tobie Basiu wyszło, że liczb podzielnych na 6 jest 84. Później od 84−17 czyli 67. Wykładowca podał 70. Jego błąd? Prosiłbym jeszcze jakieś obeznane osoby o sprawdzenie rozwiązania Basi.

Basia: a₁ = 0 r=6 500:6 = 83 reszta 4 a_n = 6*83 = 498 498= 0+(n−1)*6 498 = 6n − 6 6n = 504 n = 84 i nie ma inaczej

Tomek: W takim bądź razie widzę, że z jego tytułami naukowymi dodali mu możliwość tworzenia własnych rozwiązań w matematyce. Basiu, mógłbym Cię prosić jeszcze o rozwiązanie zadania. "Mamy liczby całkowite naturalne 100 ≤ x ≤ 999 Ile jest liczb w tym zbiorze podzielnych przez 13 lub 15 lub 17?

Garth: Mozesz obliczyc, ile jest liczb podzielnych przez 13 w tym przedziale, pozniej przez 15, a pozniej przez 17. Nastepnie przy sumowaniu wszystkich sprawdz, czy istnieja takie, ktore sa jednoczesnie podzielne przez 2 lub 3 z tych liczb, zeby nie policzyc ich dwu lub trzykrotnie.

Tomek: https://picasaweb.google.com/lh/photo/8wBrc_1c1boSjYggr96HmdMTjNZETYmyPJy0liipFm0?feat=directlink Czy to jest prawidłowe rozwiązanie? 60 + 52 + 46 + 3 + 4 + 5 = 170

Basia: tak samo musisz to robić 100:13 = 7 reszta 9 czyli najmniejsza podzielna przez 13 to 13*8 = 80+24 = 104 999:13 = 76 reszta 11 czyli największa podzielna przez 13 to 13*76 = 988 a₁ = 104 r=13 a_n = 988 a_n = a₁+(n−1)*r 988 = 104+(n−1)*13 988 − 104 = 13n − 13 884+13 = 13n 897 = 13n n = 69 podzielnych przez 13 masz 69 teraz policz ile jest w przedziale <100;999> podzielnych przez 15 a ile podzielnych przez 17 podaj wyniki to sprawdzimy

Tomek: Basiu: https://picasaweb.google.com/lh/photo/8wBrc_1c1boSjYggr96HmdMTjNZETYmyPJy0liipFm0?feat=directlink Czy to jest prawidłowe rozwiązanie? 60 + 52 + 46 + 3 + 4 + 5 = 170

Basia: nie wiem; musiałabym liczyć; a byłoby wskazane żebyś Ty sam coś policzył jeżeli masz to zrozumieć będę brutalna, ale prawda jest taka, że bez zrozumienia takich zagadnień nie masz czego szukać na informatyce

Basia: na oko wygląda poprawnie, ale nie liczyłam dokładnie

Tomek: To rozwiązanie Basiu co Ty przedstawiłaś rozumiem. Dla liczb podzielnych przez 15 w zbiorze <100;999> jest: a₁=105 (7*15) a₂=120 (8*15) r=15 a_n=990 (66*15) 990=105+(n−1)*15 990−105=15n−15 885+15=15n 900=15n n=60 Dla liczb podzielnych przez 17 w zbiorze <100;999> jest: a₁=102 (6*17) a₂=119 (7*17) r=17 a_n=986 (58*17) 986=102+(n−1)*17 986−102=17n−17 884+17=17n 901=17n n=53

Tomek: I taki sposób jest dla mnie w 100% zrozumiały. Jednak rozwiązanie mojego prof. nadzw. dr hab dla tego zadania wygląda tak: https://lh6.googleusercontent.com/-Bg68FYOXWkI/UicXjnHm2iI/AAAAAAAAAHo/SVKF1ZVy86o/w1149-h862-no/IMG_20130904_131735.jpg I kto ma rację?

Basia: ilość podzielnych przez 15 i ilość podzielnych przez 17 policzyłeś dobrze więc niestety gołym okiem widać, że rozwiązanie z ostatniego linku poprawne nie jest błędy rachunkowe się wkradły

miś: https://matematykaszkolna.pl/forum/211802.html

Tomek: No i kto mu nadał te tytuły naukowe? Dzwonie do prezydenta...

Tomek: I jak tu człowiek ma zdać przedmiot, podczas gdy licząc poprawnie oblewamy ?

Tomek: Czyli wychodzi że rozwiązanie podane przez Basie i dokończone przeze mnie jest poprawne,a profesor się pomylił.

Basia: tak nie jest i raczej nie będzie to zapewne było na wykładzie albo na ćwiczeniach; człowiek się śpieszył stąd błędy zadania egzaminacyjne zawsze są dokładnie i spokojnie wcześniej policzone poza tym swoją pracę zawsze można sprawdzić

Tomek: No tak wkradły się błędy.... To zadanie: "Podanie wszystkich liczb naturalnych podzielnych przez 2,3,5 nie większych niż 500. Wiem tylko tyle że tych liczb (naturalnych, nie większych niż 500 jest 501)." Podawał on nam rozwiązanie wczoraj na konsultacjach − według Was, forumowiczów − błędne. Zadanie: "https://lh6.googleusercontent.com/-Bg68FYOXWkI/UicXjnHm2iI/AAAAAAAAAHo/SVKF1ZVy86o/w1149-h862-no/IMG_20130904_131735.jpg" Podane przez niego na powtórce przed egzaminem też błędne. Ileż tych błędów?..

Tomek: Później człowiek siedzi i próbuje się czegokolwiek z notatek nauczyć i ma mętlik w głowie bo wyniki z kosmosu się biorą. W każdym bądź razie dziękuje bardzo wszystkim za pomoc.

Basia: to jeszcze nie koniec teraz musisz policzyć: ilość podzielnych przez 13*15 = 195 ilość podzielnych przez 13*17 = 221 ilość podzielnych przez 15*17 = 255 ilość podzielnych przez 13*15*17 = 3315 (takich w tym przedziale nie ma) |A∪B∪C| = |A|+|B|+|C|−|A∩B|−|A∩C|−|B∩C|+|A∩B∩C|

Basia: No to rozpisz elegancko (bardzo dokładnie i czytelnie) własne. I idź z nim do pana doktora.

Tomek: Basiu, a jaka jest różnica pomiędzy liczbami podzielnymi przez 2 i 3 i 5 albo podzielnymi przez 2 lub 3 lub 5?

Tomek: Dobra już wiem