Zadania z matmy kamel: Witam wszystkich chciałbym prośić o zrobienie z wytłumaczeniem dwóch zadań 1)wykonaj działania:

2		4x		1
	+		−
x−3		x+2		3

	2x+4
2)Naszkicuj wykres funkcji i omów jej własności y =
	x+3

wykres naszkicuje i omówie własności tylko ze tą funkcje trzeba chyba przekształcic do postaci kanonicznej a nie wiem jak to zrobić 2 sposobem prostszym bo wydaje mi się ze można tu podzielic wielomiany i otrzyma się wzór w postaci kanonicznej ale prosiłbym o wytłumaczenie tego 2 sposobu na tym przykładzie

Bogdan: Dzień dobry.

	3		5		1
1) Zrób to samo, co zrobiłbyś w tym działaniu:		+		+		= ...
	4		6		8

2) Podziel 2x + 4 przez x + 3 tak, jak dzieli się wielomiany.

kamel: Tak ale ja jestem kompletna noga jeśli chodzi o działania na wyrażeniach wymiernych więc badzo prosiłbym o rozpisanie chociaż tego 1 a w 2 ma wyjść

	2
−		?
	x+3

aga: cześć pierwsze zadanie musisz sprowadzić te ułamki do wspólnego mianownika czyli: U{2*3*(x+2)+4x*3*(x−3)−1*(x−3)*(x+2){(x−3)*(x+2)*3}=U{6x+12+12x²−36x−(x²+2

	11x2−29x+18
x−3x−6)}{(x−3)*(x+2)*3}=		nie wiem czy masz to jeszcze jakoś
	(x−3)*(x+2)*3

inaczej zapisać można w liczniku obliczyć Δ; Δ=29−4*11*18=49 √Δ=7

	29−7
x=		=1
	2*11

	29+7		18
x=		=
	2*11		11

	18   (x−1)(x− )   11
otrzymamy wtedy że ten ułamek=
	(x−3)*(x+2)*3

aga: a co do zadania drugiego to nie za bardzo wiem jak z tą postacią kanoniczną rozwiązała bym je w ten sposób że na początku określasz dziedzinę funkcji czyli x∊R−{−3}, ponieważ nie dzieli się przez 0, rysujesz tabelkę wpisując w niej róźne wartości x podstawiając do wzoru obliczasz y, zaznaczasz punkty w układzie współrzędnych i gotowe

Eta: masz prezent ode mnie kliknij tu 21072

Eta: Przepraszam , to miała być wskazówka dla kogoś innego.

Eta: To dla aneta33 kliknij 21072

kamel: Dzięki aga jesteś super

Bogdan:

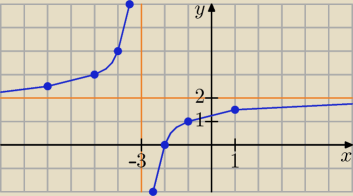
	2x + 4
y =		, założenie: x ≠ − 3
	x + 3

Wykonujemy dzielenie: 2 −−−−−−−−− (2x + 4) : (x + 3) −2x − 6 −−−−−−− −2

	2x + 4		−2
y =		⇒ y =		+ 2,
	x + 3		x + 3

1. Dziedzina D: x ∊ R \ {−3}. 2. Zbiór wartości funkcji ZW: y ∊ R \ {2}. 3. Asymptota pozioma: y = 2, asymptota pionowa x = −3. 4. Monotoniczność: funkcja jest rosnąca dla x ∊ (−∞, −3)∪(3, +∞). 5. Znak funkcji: y < 0 dla x ∊ (−3, −2) y = 0 dla x = −2 (miejsce zerowe), y > 0 dla x ∊ (−∞, −3)∪(−2, +∞) Uwaga − w rozwiązaniu ukryłem błąd, zapraszam do jego wskazania

aga: proszę bardzo

tim: Ja wiem Gdzie błąd

aga: Ja też

kamel: Sądzę że błąd jest w monotoniczności funkcja nie rośnie od 3

kamel: Bardzo dziękuje też Bogdanowi

Bogdan: Nikt dotąd nie wskazał ukrytego przeze mnie błędu. Zapraszam do poszukiwań i do podania go.

Kalumniatoris: y = 0 dla x = −2 i x = −3 Wydaje mi się że to jest ten błąd. (tak powinno być)

Bogdan: Nie Kalumniatoris, tu jest dobrze, dla x = −2 funkcja przyjmuje wartość 0, dla x = −3 funkcja nie jest określona i takie informacje podałem w opisie własności funkcji. Dodam, że błąd, który zamieściłem, jest bardzo poważny.

Kalumniatoris: **** nie zauważyłem wykresu (tak mało rzucał się w oczy)

Eta: funkcja jest rosnąca w całej dziedzinie zatem w przedziałach x€ ( −∞, −3) U( −3, ∞)

Bogdan: Tak Eto, rzeczywiście powinien być minus przed trójką, zgubiłem go, ale nie ten błąd miałem na myśli. Błąd jest w zapisie przedziału monotoniczności, powinno być tak: funkcja jest rosnąca dla x ∊ (−∞, −3), (−3, + ∞). Nie może być znak sumy zbiorów ∪, tu musi być przecinek.

Eta: Też coś? pierwszy raz coś takiego widzę kto to wymyślił jeżeli D= R\{−3} = [ ( −∞, −3) U( −3, ∞)] to jest równoważne sumie przedziałów otwartych zawsze tak uczyłam ( i mnie też tak uczono ) Czy możesz mi wyjaśnić ; co ma oznaczać przecinek ?

Eta: AROB Co TY na to To jakieś dziwactwa ( tak ja uważam)

Eta: Przepraszam ,ale mnie trochę "poniosło" !

Eta: Czy to są może "normy" Unii Europejskiej w matematyce

AROB: Ja też, Eta, byłam uczona przed "wiekami" tak, jak Ty. A od kilku lat zmuszona byłam się przestawić na wersję z przecinkami, choć bez przekonania. Spotkałam uzasadnienie tej teorii, ale dziwnie to brzmi , mimo wszystko.

Eta: he,he..... w takim układzie , muszę uciekać z forum ,bo nigdy się nie przekonam do takiego zapisu! Pora spać Dobranoc, miłych snów

Bogdan: Za późno jest już na wyjaśnienie, w dzień wrócimy do tego zagadnienia. Dodam jedynie, że korzystamy tu wprost z definicji funkcji rosnącej względnie z definicji funkcji malejącej.

AROB: Masz rację Eta! Jak można tak zmieniać przedmiot ,,jakby nie było, ścisły! Podobny dylemat przeżyłam z odczytywaniem przedziałów monotoniczności z wykresu: zawsze były otwarte, a teraz jedni domykają, inni nie, więc wprowadzono absurdalne "przedziały maksymalne" . . Lepiej idźmy spać, szkoda nerwów przed snem! Dobranoc!

Bogdan: Dobranoc Eto i AROB

AROB: DobranocBogdanie Dość na dziś!

Eta: W ciągu ostatnich 45 minut na forum pojawili się: Eta, AROB, Bogdan Dobranoc wytrwałej "trójcy"

Eta: Jeszcze dorzucę: ta godzina i ten "skład" świadczy wybitnie o "skrzywieniu zawodowym"

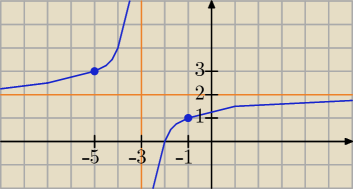
Bogdan: Definicja funkcji rosnącej. Funkcja f(x) jest rosnąca w przedziale A wtedy, gdy z założenia x₂ − x₁ > 0 wynika f(x₂) − f(x₁) > 0. Definicja funkcji malejącej. Funkcja f(x) jest malejąca w przedziale A wtedy, gdy z założenia x₂ − x₁ > 0 wynika f(x₂) − f(x₁) < 0.

	−2
Weźmy funkcję f(x) =		+ 2 i jej wykres.
	x + 3

Niech A = R \ {−3}, A jest dziedziną tej funkcji. A: x ∊ (−∞, −3)∪(−3, +∞) Przyjmujemy: x₁ = −5 ∊ A, x₂ = −1 ∊ A. Widzimy, że −1 − (−5) = 4 > 0, czyli x₂ − x₁ > 0, spełnione jest więc założenie określone w definicji funkcji rosnącej oraz w definicji funkcji malejącej. Wyznaczamy teraz znak różnicy: f(x₂) − f(x₁), jeśli ta różnica jest dodatnia, to funkcja jest rosnąca w przedziale A, a jeśli jest ujemna, to funkcja jest malejąca w tym przedziale.

	−2		−2
f(x1) =		+ 2 ⇒ f(−5) =		+ 2 = 3
	x1 + 3		−5 + 3

	−2		−2
f(x2) =		+ 2 ⇒ f(−1) =		+ 2 = 1
	x2 + 3		−1 + 3

f(x₂) − f(x₁) = 1 − 3 = −2 < 0, czyli funkcja jest malejąca, co jak widać na rysunku, jest nieprawdą. Sprzeczność wynikła z przyjęcia przedziału A = (−∞, −3)∪(−3, +∞), czyli przyjęcia sumy przedziałów. Uniknie się sprzeczności, jeśli przeprowadzimy badanie monotoniczności funkcji oddzielnie dla przedziałów: A₁ = (−∞, −3) oraz A₂ = (−3, +∞). Poprawny zapis przedziałów monotoniczności dla rozpatrywanej funkcji może być taki: f(x) ↗ dla x ∊ (−∞, −3), f(x) ↗ dla x ∊ (−3, +∞); Dopuszcza się skrócone formy zapisu: f(x) ↗ dla x ∊ (−∞, −3), (−3, +∞) albo jeszcze krócej: ↗ (−∞, −3), (−3, +∞). Podsumowując. Monotoniczność opisujemy oddzielnie dla każdego przedziału będącego składnikiem sumy przedziałów tworzących dziedzinę funkcji. Nie można przedziałów łączyć znakiem sumy zbiorów ∪.

Bogdan: Dzień dobry AROB i Eto .

żółwik:

Bogdan: żółwiku, rozpoznałem Ciebie Eto

żółwik: Dzień dobry, witam "Sherlock Holmes"

żółwik: http://tygodnik.onet.pl/30,0,33936,produkcja_uniwersytecka,artykul.html Bogdanie, świetny artykuł polecam .......

Bogdan: Przeczytałem i podzielam zamieszczone poglądy w artykule. Interesujące są również komentarze znajdujące się pod tekstem artykułu. Kiedyś, jakieś 40 lat temu, jeden z popularnych w tamtych czasach publicystów zauważył: " ... my, ćwierćinteligenci, jesteśmy solą tej ziemi ...". Myślę, że to spostrzeżenie jest dzisiaj również aktualne, niestety. Dobrze jednak, że zauważa się zjawisko opisane przez autorkę artykułu.

żółwik: