dwa zadania ze stereometrii- pomocy! karmelka: zadanie 1. Podstawą ostrosłupa jest trapez równoramienny o podstawach a i 3a. Ściany boczne tworzą z płaszczyzną podstawy kąt α. Obliczyć objętość ostrosłupa. zadanie 2. Wyznacz kąty dwuścienne (wszystkie) takiego ostrosłupa, którego podstawą jest trójkąt równoboczny, a krawędzie boczne są parami do siebie prostopadłe. ( z tego co się orientuję przy wierzchołku ostrosłupa jest kąt 90 stopni chyba). Proszę o pomoc w rozwiązaniu, albo jakieś wskazówki czy pomysły, będę bardzo wdzięczna nawet za "luźne" pomysły jakby można to było rozwiązać, może być bez żadnych obliczeń tylko od czego zacząć, ewentualnie z jakich wzorów czy twierdzenia korzystać bo ja nie mam pomysłu obojętne do którego zadania, czy do jednego, czy do dwóch, każda pomoc się przyda Z góry wielkie dzięki za każdą próbę pomocy

karmelka: proszę ludzie pomocy jakiekolwiek sugestie

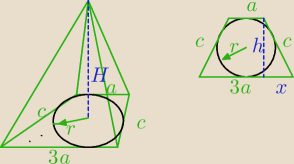
dero2005: Jeżeli ściany są pochylone pod kątem α to w podstawę można wpisać okrąg

	3a−a
x =		= a
	2

3a+a = 2c → w czorokącie opisanym na okręgu suma przciwległych boków jest równa 4a = 2c c = 2a h² = c² − x² h = a√3

	h		a
r =		=		√3
	2		2

	3a+a
Pp =		*h = 2a2√3
	2

H
	= tgα
r

	a
H = r*tgα =		√3tgα
	2

	Pp*H
V =
	3

karmelka: dzięki zaraz przeanalizuję i spróbuję zrozumieć bo wygląda dość prosto

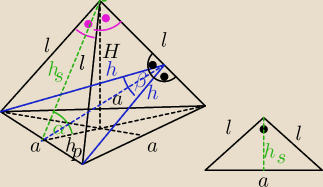
dero2005: a² = 2l²

	a√2
l =
	2

	a
hs =
	2

	a√3
hp =
	2

	1   hp 3
cosα =
	hs

h*l = a*h_s

	a*hs
h =
	l

a² = 2h² − 2h²*cosβ cosβ =

karmelka: Niestety co do pierwszego zadania to jest jednak haczyk i nie mogę się zgodzić. na jakiej podstawie w trapez wpisałeś okrąg? W treści zadania nie jest podane że suma przeciwległych boków jest równa (suma długości podstaw wcale nie musi być równa sumie długości ramion trapezu), a tylko w takim wypadku w trapez można wpisać okrąg. A co jeżeli właśnie nie będzie się dało wpisać w trapez okręgu (bo z treści zadania wcale to nie wynika). Może jakieś inne pomysły do tego zadania Bo niestety ta metoda mnie nie zadowala

karmelka: bo gdyby nie to, zadanie byłoby bardzo proste. Chyba że źle zrozumiałam polecenie,albo zauważyłeś jakoś że na pewno da się wpisać okrąg, to proszę o wyjaśnienie jak

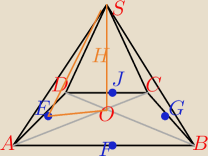
karmelka: dobra już wiem, zadanie jest jednak dobrze rozwiązane (chyba). Może mi ktoś powiedzieć czy dobrze rozumiem− jeżeli na wszystkich ścianach bocznych poprowadzimy wysokości i połączymy je ze spodkiem wysokości ostrosłupa O, i kąty przy wierzchołkach E,F,G,J powstałych (po połączeniu) trójkątów będą miały taką samą miarę α, to trójkąty ΔEOS, ΔFOS, ΔGOS i ΔJOS będą przystające tak (cecha kąt(90 stopni)−bok(wysokość H)−kąt(α)) wtedy znaczyłoby że da się wpisać okrąg. Dobrze zrozumiałam Mógłby się ktoś wypowiedzieć?

dero2005: jezeli wszystkie kąty pochylenia płaszczyzn bocznych do podstawy są równe to w podstawę musi

	H
byc mozliwość wpisania okręgu, wtedy tgα =
	r

gdzie H−wysokość ostrosłupa,, r − promień okręgu wpisanego

dero2005: 874

Mila: Karmelko, popatrz na rozwiązanie zadania (1), rysunek trapezu z prawej strony. Punkty styczności okręgu wpisanego w trapez nie leżą w środkach ramion.

karmelka: ok , już widzę

Mila: 1) W ostrosłupach prawidłowych środek okręgu opisanego na podstawie pokrywa się ze środkiem okręgu wpisanego w podstawę i jest spodkiem wysokości ostrosłupa. 2) Jeżeli w ostrosłupie wszystkie krawędzie boczne są równe to spodek wysokości znajduje się w środku okręgu opisanego na podstawie. 3)Jeżeli w ostrosłupie wszystkie krawędzie boczne są nachylone pod tym samym kątem do płaszczyzny podstawy to spodek wysokości znajduje się w [N[środku okręgu opisanego na podstawie]]. 4) Jeżeli w ostrosłupie wszystkie ściany boczne są nachylone pod tym samym kątem do płaszczyzny podstawy to spodek wysokości znajduje się w środku okręgu wpisanego w podstawę.

karmelka: ok dzięki nie wiedziałam tego z nachyleniem ścian bocznych dzięki za pomoc

Mila: