jednokładnosc ble ble: Czy ktoś pomoze mi to rozwiazac? Dany jest trójkat ABC w którym A(−1,−1) B(6,−1) C(3,3). trojkat A'B'C' jest obrazem trojkata ABC w jesnokładnosci 3, gdzie O(0,0). Oblicz obwody trojkatow. Ile razy obwod trojkata A'B'C' jest większy od obwodu trojkata ABC?

wredulus_pospolitus: I w czym konkretnie masz problem obwód ABC potrafisz obliczyć co oznacza, że coś jest obrazem w jednokładności 3 (podpowiem −−− skali 3)

Basia: w jednokładności o środku O(0,0) i skali 3 czy nawet treści z książki nie można poprawnie przepisać ? policz |AB|, |AC|, |BC| i dodaj długość odcinka − patrz https://matematykaszkolna.pl/strona/1248.html Ob_A'B'C' = 3*Ob_ABC

ble ble: ale właśnie tak wychodzą jakies bzdury..

Basia: zdaje mi się, że w tym zadaniu jednak chodzi o policzenie współrzędnych A',B' i C' policzenie długości |A'B'|, |A'C'|, |B'C'| i sprawdzenie jak się ma Ob_A'B'C' do Ob_ABC takie wprowadzenie do uogólnienia, że |A'B'| = |k|*|AB| gdzie k jest skalą jednokładności

Basia: zapisz swoje obliczenia, poszukamy tych bzdur najpierw |AB|; czekam

ble ble: a jak bym to z wektorow zrobila?

Basia: A',B' i C' tylko przy pomocy wektorów ale najpierw masz policzyć obwód ABC

ble ble: bo ja tak zrobiłam : AB=[6− (−1);−1− (−1)]=[7;0]

Basia: dobrze ; no to |AB| = √7²+0² = 7 licz dalej w ten sposób

ble ble: później BC=[9;4] CB=[4;4] dodałam wszystkie wektory i wyszło mi AC + BC + AB =[20;8]

ble ble: IBCI=13 IACI=8 i co dalej?

Mila: 1) oblicz obwód ΔABC 2) obwód ΔA'B'C' jest 3 razy większy od obwodu ΔABC. 3) jeśli masz obliczyć wsp .ΔA'B'C' to : A'=(3*(−1),3*(−1))=(−3,−3) pozostałe punkty podobnie.

ble ble: a jak policzyłam nie punkt tylko odcinek to jest blad czy tak może byc ?

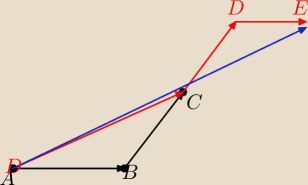
Basia: a nie to już nie ma sensu obwód nie ma nic wspólnego z wektorami Ty policzyłaś współrzędne tego niebieskiego wektora zakładam, że CD = BC i DE = AB, bo na rysunku nie bardzo mi wyszło poza tym współrzędne BC masz źle policzone BC = [−3; 4] |BC| = √9+16 = 5 AC = [4;4] |AC| = √16+16 = 4√2 Ob_ABC = 7+5+4√2 = 12+4√2

Basia: co Ty tam wypisujesz ? u^→=[u₁;u₂] to |u| = √u₁²+u₂²

ble ble: aha no okey dzięki

Mila: Basia napisała,że masz niedokładnie przepisaną treść zadania. Należy wykonać to, co jest w poleceniu. Odcinki ( długości boków Δ) potrzebne do obliczenia obwodu. Możesz wykonać jak napisałam (1) (2) albo pomnożyc przez 3 długość każdego boku ΔABC i dodać. albo obliczyć wsp. wierzchołków ΔA'B'C', obliczyć długości boków i obwód. Wybierz najkrótszy sposób.

Mila: Wyłączam się, bo jest Basia.