Wielomian bezendu: Dany jest wielomian W(x)=(x²+3x−4)(x−t) wyznacz wszystkie wartości parametru t takie aby spełniona była nierówność W(0)>0 W(x)=(x²+3x−4)(x−t) Δ=25 √Δ=5

	−3−5
x1=		=−4
	2

	−3+5
x2=		=1
	2

W(x)=(x−1)(x+4)(x−t) Co dalej mam z tym zrobić ?

Mila: 1) oblicz w(0) i analizuj albo 2) skoro masz 2 pierwiastki , rozwiązuj na osi.

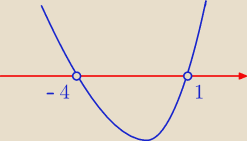
bezendu: I teraz to ma być większe od zera x∊(−∞,−4)∪(1,∞) o to chodziło ?

bezendu: ?

Mila: 1) w(0)=−4*(−t)=4t 4t>0→t>0 Graficznie pokazać?

bezendu: Tak, ponieważ nie rozumiem od momentu rozłożenia na postać iloczynową..

pigor: ..., zauważ, że W(x)= (x−1)(x+4)(x−t) ⇒ W(0)= −1*4*(−t)= 4t >0 ⇔ t >0 ⇔ t∊(0;+∞) i tyle .

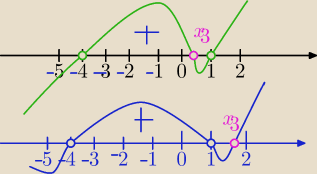
Mila: O, już wyjaśnione. Nie trzeba było liczyc miejsc zerowych. Jednak można to wykorzystać. Graficznie, to raczej utrudnia, ale może przyda się do innego zadania. (mam gdzieś takie zadanie, znajdę dla Ciebie) Dla zera wartość dodatnia , zatem trzeci pierwiastek może być po prawej stronie zera

bezendu: Dziękuje

Mila: ładnie rozwiązałeś z wartością bezwzględną.

bezendu: Dziękuje staram się jak mogę

bezendu: Mila masz jakieś zadanie z dzieleniem wielomianów coś w tym stylu https://matematykaszkolna.pl/strona/2902.html ? bo w piątek mam już sprawdzian z wyrażeń algebraicznych i chciałbym spróbować na wyższą ocenę

Saizou : http://www.zadania.info/d413/1/0.2_0.5 może być

bezendu: Może być Najpierw jeszcze wstawię swoje

bezendu: Wyznacz wartości parametrów a i b występujących we wzorze wielomianu W(x)=(a+b)x³−2x²+(a+2b)x wiedząc że reszta z dzielenia W(x) przez x−2 jest równa 18, zaś reszta z dzielenia wielomianu W(x) przez x+1 jest równa −6 (a+b)*8−8+(a+2b)*2=18 −a−b−2−a−2b=−6 8a+8b−8+2a+4b=18 −2a−3b=−4 10a+12b=26 /2 −2a−3b=−4 5a+6b=13 −2a−3b=−4 / *2 5a+6b=13 −4a−6b=−8 a=5 −10−3b=−4 −3b=6 b=−2 Wiem, że na maturze nikt mi ni sprawdzi i muszę liczyć sam na siebie, ale chodzi o sprawdzenie zapisu i może jakiś inny sposób rozwiązania

bezendu: Wyznacz wartość parametrów a i b tak aby wielomian W(x)=x³+(a+2b)x²−x(a+b) był podzielny przez dwumian x²−1 x²−1=(x−1)(x+1) Aby był podzielny to W(1)=0⋀W(−1)=0 1+a+2b−a−b=0 b=−1 −1+a+2b+a+b=0 2a+3b=1 2a−3=1 2a=4 a=2 Odp a=2 i b=−1

ICSP: a+2b = 0 a+b = 1 skąd dostajesz a = 2 , b = −1

bezendu: ICSP zerknij jeszcze na zadanie 21:53

ICSP: wygląda dobrze

Mila: 21:53 Dobrze, możesz podstawić do wielomianu otrzymane wartości i sprawdzić w(2) i w(−1), to będzie samokontrola.

merto: zad z 21:53 ok Na wstępie należało napisać: Warunki zadania są spełnione dla układu równań W(2)=18 i W(−1)= −6 Odp: a= 5 i b= −2 sprawdzenie: W(x)= 3x³ −2x² +x W(2)= 3*8−2*4+2= 18 ok W(−1)= −3−2−1 = −6 ok i bez pytania ............ jest ok

bezendu: Dziękuje