Planimetria bezendu: https://matematykaszkolna.pl/strona/3220.html Czy można zrobić to zadanie jakimś innym sposobem, nie korzystając z podobieństwa trójkątów ?

Mila:

	3
cos β=
	5

|BM|=20 z tw. cosinusów: |CM|²=30²+20²−2*20*30*cosβ dokończ

bezendu: |CM|²=580 |CM|=2√145 lub |CM|=−2√145∉R₊

bezendu: Czyli każde zadanie da się obejść bez podobieństwa trójkątów ?

Godzio:

	3
cosα =
	5

	a + b − c
r =		= 10
	2

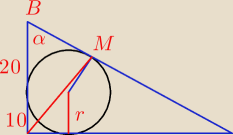
|MB| = 10 (wynika to, że odcinki od punktu przecięcia do punktu styczności są równe) I z twierdzenia cosinusów: x² = 30² + 20² − 2 * 30 * 20 * cosα = 1300 − 720 = 580, stąd x = 2√145

Godzio: |MB| = 20 oczywiście

bezendu: Dziękuje

Godzio: Na 95% powiem, że każde. Nie zawsze jest to krótsza droga, ale pewnie się da

bezendu: Ale ja bardzo nie lubię tego, wole twierdzenie sinusów lub cosinusów i w tym wypadku szybsze