Znajdz x
sebi: znajdz x
log x=1
20 sie 21:31
bezendu:
x=10
20 sie 21:32
sebi: no ale jak to ?
20 sie 21:33
bezendu: to jest logarytm dziesiętny i przy podstawie zawsze ma 10, wiec
log10x=1
log1010=1
20 sie 21:38
sebi: acha

widzisz teraz ogarniam jak przy podstawie nie ma nic to zawsze jest 10 ?
20 sie 21:39
Garth:
Dziedzina: x > 0
log10x = 1 ⇔ 101 = x ⇔ x = 10
20 sie 21:40
Garth:
log(b) = log10(b), innymi slowy − tak.
20 sie 21:40
sebi: Słiuchajcie dobrze

log x=−2 −−−>x= 10
−2 = 1
1102
20 sie 21:47
5-latek: Tak.
Przy takim zapisie przyjmuje sie ze posdstawa takiego logartmu jest 10
czyli bedzie to logarytm dziesietny .
Przy zapisie takiego logarytmu tej 10 w podstawie sie nie zapisuje ale trzeba o tym pamietac
Czyli nasz logarytm mozemy zapisac tak log
10x=1
Definicja logarytmu mowi log
ab=c to b=a
c −odpowiednie zalozenia co do poddstawy i liczby
logarytmowanej musza byc)
Unas a=10 b=x a c=1 wiec z tej definicji b=a
cto b=10
1=10
https://matematykaszkolna.pl/strona/217.html Tutaj definicja logarytmu

20 sie 21:47
20 sie 21:48
20 sie 21:51
bezendu:
| | 1 | |
5−latek chyba zapis nie tak, powinno być ( |
| )2 |
| | 10 | |
| | 2 | | 2 | |
no jak byś miał ( |
| ) to |
|   wiem że tam jest jedynka ale... |
| | 10 | | 102 | |
20 sie 21:55
sebi: Słuchaj no dobra a taki jak ten jak zrobic ?
log √3x=12
20 sie 21:56
bezendu:
tak jak pozostałe

20 sie 21:57
Garth:
| | 1 | | a | | b | |
bezendu: a−n = |
| , ( |
| )−n = ( |
| )n |
| | an | | b | | a | |
20 sie 21:59
bezendu:
| | 2 | |
( |
| ) −2  |
| | 5 | |
20 sie 22:00
Garth:
| | 1 | |
log√3x = |
| ⇔ 10 12 = √3x ⇔ ... dokoncz  |
| | 2 | |
20 sie 22:01
Garth:
| | 2 | | 25 | |
( |
| )−2 = |
| ...z zapisem 5−latka wszystko w porzadku.  |
| | 5 | | 4 | |
20 sie 22:03
sebi: ale to już nie jest ten dziesiętny...
20 sie 22:03
Garth: To zapisz wyrazniej, co jest podstawa, bo wyglada na dziesietny.

Mozesz zapisac w ten sposob: log
a(b), gdzie a jest podstawa, a b liczba logarytmowana.
20 sie 22:05
sebi: log a to pierwiastek z 3 x = 1/2
20 sie 22:07
Garth:
Jesli dobrze rozumiem masz na mysli:
| | 1 | |
log√3(x) = |
| ⇔ (√3)12 = x ⇔ (312)12 = x ⇔ |
| | 2 | |
⇔ x = 3
14 ⇔ x =
4√3
Dziedzina: x > 0
20 sie 22:15
5-latek: bezendu a jaka jest roznica miedzy naszymi zapisami . Zadnej
| | 2 | | 5 | | 52 | | 25 | | 1 | |
( |
| )−2=( |
| )2= |
| = |
| =6 |
| =6,25  |
| | 5 | | 2 | | 22 | | 4 | | 4 | |
20 sie 22:16
Garth:
Jezeli nie czujesz sie pewnie z potegami i pierwiastkami, lepiej najpierw sie do tego przyloz i
dobrze wycwicz liczenie ich. Bo bez tego ciezko bedzie z logarytmami.

20 sie 22:16
Garth:
sebi, masz tu przyklad, sprobuj go obliczyc [pamietaj o wyznaczeniu dziedziny]:
logx(512) = 9
20 sie 22:18
sebi: tego nie oblicze ja robiłem takie proste bardziej.
20 sie 22:21
Piotr 10: x=2
20 sie 22:23
sebi:
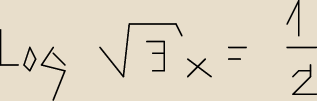
20 sie 22:23
sebi: tak wygląda ten moj przykład. dokładnie x nie jest w nawiasie.
20 sie 22:24
Garth: To jest proste.

Probuj, tylko pamietaj wlasnie o wyznaczeniu dziedziny.
log
a(b)
Warunki dla podstawy: a > 0 ∧ a ≠ 1
Warunki dla b: b > 0
20 sie 22:24
Garth: Nadal nic nie wiadomo z tego Twojego logarytmu. Podstawe zapisuje sie w indeksie dolnym.
Czy chodzilo o:
| | 1 | |
log√3x = |
| , gdzie wyrazenie √3x to podstawa logarytmu? |
| | 2 | |
20 sie 22:26
sebi: tak to jest w indeksie dolnym.
20 sie 22:27
5-latek: Garth widzialem tez ze uczysz sie logarytmow
jest tez taki fajny wzorek do logarytmow
| | 1 | |
logan z b= |
| logaz b a ten wzor to podstawa logabn=nlogab |
| | n | |
Wiec wezmy taki przyklad
| | 2 | | 13 | | 26 | | 26 | |
log33/2 313/3= |
| * |
| *log33= |
| *1= |
| |
| | 3 | | 3 | | 9 | | 9 | |
Mozna bylo tez zapisac
√3=3
1/2 i z tego pierwszego wzoru co i podalem liczyc dalej .Moze
sie przyda

20 sie 22:40
5-latek: | | 1 | | 1 | |
Moze tak zapisane log√3x= |
| czyli logarytm przy podstawie √3 z x= |
| |
| | 2 | | 2 | |
20 sie 22:46
Garth:
| | 1 | |
Znam to, chociaz moze nie za czesto uzywam tego: logan(b) = |
| loga(b), wiec dzieki za |
| | n | |
przypomnienie.

Chyba czas zaczac sie nim czesciej bawic.

20 sie 22:46
5-latek: Bo jesli bedzie √3x to podstawa logarytmu to wtedy to wyrazanie jest bez sensu bo nie ma
liczby logarytmowanej
20 sie 22:50
Mila:
logam(bm)=loga(b)
np.
log2(3)=log4(9)
log2(4)=log8(64)
20 sie 23:41
asdf: Zadanie dla
Garth, wyprowadź wzór:
a
logab = b

20 sie 23:50
Saizou : asdf to wynika z definicji logarytmu
logab=c jeżeli ac=b
b=alogab
21 sie 00:01
asdf: brawo Garth, dobrze Ci poszło


21 sie 00:03
asdf: i dziękuje, że mi to wyprowadziłeś, bo nie wiedziałem...
21 sie 00:04
Saizou : gomene, ale takie fajno było

21 sie 00:05
Garth:
log
ab=c ⇔ a
c = b ⇔ a
logab = b

21 sie 00:06
Saizou : a i tak przy okazji, nie musisz podchodzić od razu tak sarkastycznie
21 sie 00:08
asdf: To nie było sarkastyczne, tylko chciałem Ci zwrócić uwagę. Garth siedział ostatnio w
logarytmach i chciałem mu "ot tak" przypomnieć lub utrwalić ten wzór.
21 sie 00:15
Saizou : " i dziękuje, że mi to wyprowadziłeś, bo nie wiedziałem..." w moim odczuciu to był sarkazm
21 sie 00:19
asdf: w moim ironia
21 sie 00:33
21 sie 00:37
asdf: 
21 sie 00:40
 widzisz teraz ogarniam jak przy podstawie nie ma nic to zawsze jest 10 ?
widzisz teraz ogarniam jak przy podstawie nie ma nic to zawsze jest 10 ?
 log x=−2 −−−>x= 10−2 = 11102
log x=−2 −−−>x= 10−2 = 11102


 wiem że tam jest jedynka ale...
wiem że tam jest jedynka ale...



 Mozesz zapisac w ten sposob: loga(b), gdzie a jest podstawa, a b liczba logarytmowana.
Mozesz zapisac w ten sposob: loga(b), gdzie a jest podstawa, a b liczba logarytmowana.


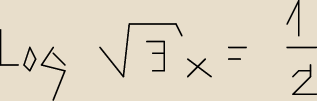
 Probuj, tylko pamietaj wlasnie o wyznaczeniu dziedziny.
loga(b)
Warunki dla podstawy: a > 0 ∧ a ≠ 1
Warunki dla b: b > 0
Probuj, tylko pamietaj wlasnie o wyznaczeniu dziedziny.
loga(b)
Warunki dla podstawy: a > 0 ∧ a ≠ 1
Warunki dla b: b > 0

 Chyba czas zaczac sie nim czesciej bawic.
Chyba czas zaczac sie nim czesciej bawic. 





