Planimetria bezendu: Czy w dowolnym trapezie zachodzi taka własność ?

a+b
	=c gdzie a i b to podstawy trapezu a c jego ramię ?
2

Patryk: to masz wtedy gdy trapez jest opisany na okręgu,i trapez jest równoramienny

bezendu: ok dzięki

Mila: Wyciągaj wnioski.

Patryk: napewno ?

Eta:

	a+b
a+b=c+c ⇒		= c
	2

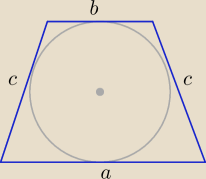
teraz na bank

Patryk:

Eta:

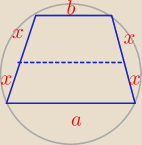
bezendu: Wykaż, że długość odcinka łączącego środki ramion trapezu równoramiennego opisanego na okręgu jest równa długości tego ramienia

a+b
	2x=c
2

a+b=2x+2x a+b=4x

4x
	=2x
2

2x=c C.N.D ok ?

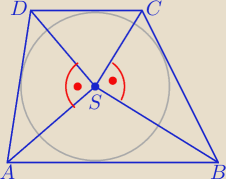
Gustlik: A ja udowodniłem bardzo ciekawą własność wszystkich trapezów opisanych na okręgu − mianowicie, że trójkąty ASD i BSC są prostokątne. Może ktoś chętny spróbuje to udowodnić? Szczerze mówiąc ta własność już kilka razy przydala mi sie w zadaniach.

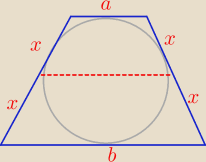
bezendu: rysunek ma wyglądać tak

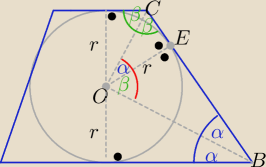
Eta: To znane twierdzenie "od wiek wieków" i bardzo przydatne 2α+2β=190^o ⇒ α+β=90^o OC i OB odcinki dwusiecznych kątów 2β i 2α trójkąty BOE i OEC są podobne Pozdrawiam "odkrywcę"

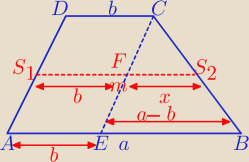
Gustlik: bezendu, to jest tzw. linia środkowa trapezu − łączy ona środki obu ramion i bez względu na to, czy jet to trapez opisany na okręgu czy nie, zachodzi wzór:

	a+b
m=
	2

Można to udowodnić z powyższego rysunku: Dzielimy trapez na równoległobok i trójkąt, widzimy ze: m=b+x Z Talesa (podobieństwo ΔEBC i ΔFS₂C) mamy:

x		1
	=
a−b		2

2x=a−b

	a−b
x=
	2

	a−b
m=b+
	2

	2b+a−b
m=
	2

	a+b
m=
	2

Czyli długość linii środkowej trapezu jest równa średniej arytemtycznej jego podstaw. c.n.d.

bezendu:

	a+b
Gustlik wiem że jest taki wzór i to jest prawdziwe dla trapezu
	2

	a+b
ale chodziło o to że		=c to miałem wykazać
	2

Gustlik: Eta Nie jestem "odkrywcą" ale wpadłem na to przy rozwiązywaniu zadań z trapezami. Ja wiem, ze to znane twierdzenie, ale zależało mi go na jego pokazaniu, bo w szkołach o nim ani widu ani słychu. Szczerze mówiąc nawet ja sobie nie przypominam, żebyśmy to w szkole ponad 20 lat temu przerabiali, choć poziom był wtedy kilka razy wyższy. Pozdrawiam.

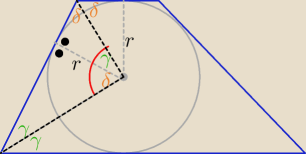
Eta: podobnie z drugiej strony

Gustlik: Ja wiem bezendu, o co Cio chodzi, to wynika z własności czworokąta opisanego na okręgu, ale mówię o tym drugim rysunku − narysowałeś linię środkową. Pozdrawiam.

bezendu: Bo pierwszy był źle i poprawiłem, oczywiście za dowód dziękuję na pewno się przyda

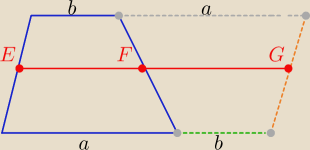
Eta: Można też tak: Mamy równoległobok o dłuższym boku a+b ( złożony z dwu przystających trapezów (odwróconych podstawami

	a+b
|EG|= a+b to |EF|=
	2

bezendu: to jest cały czas do linii środkowej trapezu ?

Eta: Sorry ... troszkę skrzywił mi się równoległobok

Eta: Tak.... chodzi o linię środkową trapezu

bezendu: Eta ''poliglota''

Eta: Co to znaczy?

bezendu: http://pl.wikipedia.org/wiki/Poliglota

Eta: Tyle to ja wiem ale co oznacza taki koment do mnie?

bezendu: Post 20:18 ''Sorry''

Eta: Aha

bezendu: Teraz jasne ?

Eta: Tak nauczyłam się tego od Was na tym forum

bezendu:

Eta:

bezendu: Eta widziałaś dziś to zadanie z trójkątem ? tydzień temu pytałem się jak to zrobić, a dziś przez dżunglę idąc zrobiłem

Eta: Nie wiem z którym trójkątem?

bezendu: https://matematykaszkolna.pl/forum/208898.html

Eta: Wektorami prościej

bezendu: Jeszcze nie znam tak dobrze wektorów, więc nie chciałem wstawiać rozwiązania na wektorach żeby kogoś wprowadzać w błąd a tym bardziej to zadanie z podstawy i tam nie ma wektorów

Eta:

bezendu: hmm a które ''zdrowe'' ?

Eta:

Eta: Pierwsze z brzegu

bezendu:

Eta: No to masz pecha "zdrowe" z prawej strony

bezendu: ale ja nie powiedziałem, które wziąłem

Eta: