gemoetria analityczna Leołoś : Dany jest trójkąt równoramienny ABC o kącie prostym przy wierzchołku C i o wierzchołkach A=(1,4) B=(7,2) Wyznaczyć współrzędne wierzchołka C tego trójkąta ? jakieś podpowiedzi ?

Mila: AB to średnica okręgu.

Leołoś : a skąd to wiadomo d=√(7−1)²+(2−4)²=2√10

Mila: Kąt wpisany oparty na średnicy jest kątem prostym ( jako połowa kąta środkowego o mierze 180⁰)

Leołoś : a nie da się tego zrobić bez okręgu ?

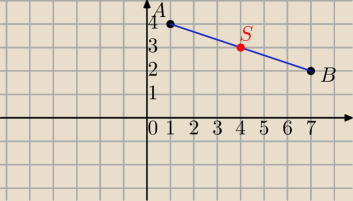
Mila: A=(1,4) B=(7,2) Da się. C=(x,y) AB jest przeciwprostokątną |AB|=[√6²+2²=√40=2√10 środek AB

	1+7
xs=		=4
	2

	4+2
ys=		=3
	2

S=(4,3) |SC|=|SB|=√10 SC⊥AB Dokończysz? Pomyśl trochę. Najlepiej wektorowo.

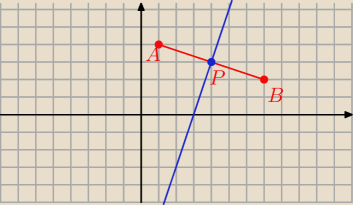
bezendu: A=(1,4) B=(7,2)

	7+1		4+2
S|AB|=		.		)=(4,3)
	2		2

prosta przez punkty A i B a+b=4 /(−1) 7a+b=2 −a−b=−4 7a+b=2 6a=−2

	1
a=−
	3

	1
7*(−		)+b=2
	3

	13
b=
	3

prosta prostopadła i przez punkt P y=3x−9 punkt c należy do tej prostej wiec ma współrzędne (x,3x−9) |AC|=2√5 (to w następnym poście ) √1−x)²+(3x−9−4)²=2√5 √x²−2x+1+(3x−13)²=2√5 √x²−2x+1+9x²−78x+169=2√5 √10x²−80x+170=2√5 /² 10x²−80x+170=20 10x²−80x−150=0 /10 x²−8x−15=0 Δ=8²−60=4 √Δ=2

	8−2
x1=		=3
	2

	8+2
x2=		=5
	2

x₁=3*3−9=0 więc x_c=(3,0) lub x₂=3*5−9=6 więc x_c=(5,6)

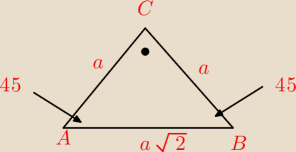
bezendu: teraz skąd tam mam 2√5 AB=2√10 a√2=10√2

	10√2
a=		=2√5
	√2

Mila sprawdź proszę czy wszystko jest ok ?

Lełoś : A jak wektorami to zrobić ?

Mila: Wektorowo: SB^→=[3,−1] SC⊥SB SC^→=[1,3] lub SC→=[−1,−3] współrzędne wektora o równej długości i prostopadłego do wektora SB S=(4,3) przesuwamy o wektor SC S=(4,3)→[1,3] →C₁=(4+1,3+3)=(5,6) S=(4,3)→[−1,−3] →C₁=(4−1,3−3)=(3,0)

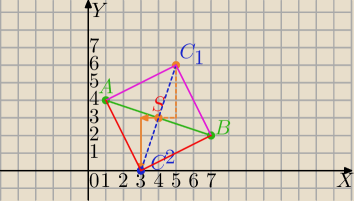
Mila: Powinno być C₂=(3,0) Popatrz jak przesunięto punkt S.

Eta:

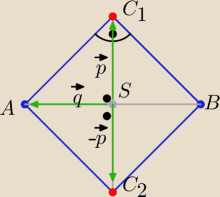
	7+1		2+4
S(		,		)= S(4,3)
	2		2

→ SA= [1−4, 4−3]= [−3,1] z warunku prostopadłości i równości wektorów p i q → p=[1,3] lub p=[−1,−3] , p=[x_c−x_S, y_C−y_S]= x_C−4, y_C−3] zatem x_c−4= 1 i y_C−3=3 lub x_C−4= −1 i y_C−3= − 3 x_C=5 i y_C=6 lub x_C= 3 i y_C=0 C₁(5,6) C₂(3,0)

Eta: Co będzie jeżeli: A(2013, 1000) , B(1201, 2000) Jak tu popatrzeć na rysunek ?

bezendu: Mila czemu c₂=(3,0) a nie (5,6) to chyba nie ma żadnej różnicy ?

bezendu: Eta ?

Mila: Bezendu, to obojętne, może być też tak jak Ty oznaczyłeś.

Eta:

bezendu: Przepraszam ja spojrzałem na post 19:12 a to było do postu 19:04

Mila: Tak, miałam kolizję oznaczeń. Odnotowałam to później.

lełoś :

Mila: O co chodzi?

lełoś : Ten sposób 18:34 bardzo długi chyba jednak lepiej to na okręgu

Mila: Sposób Bezendu można trochę skrócić. S=(4,3) |SC|=√10 to masz obliczone

	−1
AB: y=		x+b (wsp. b nie jest nam potrzebny)
	3

prosta CS: (prostopadła do AB) y=3x+b i S=(4,3)∊prostej CS⇔3=3*4+b, b=−9 y=3x−9 Punkt C leży na prostej CS i jest odległy od punktu S o √10 (⇔leży na przecięciu prostej CS i okręgu o środku (4,3) i promieniu √10) (x−4)²+(y−3)²=(√10)² y=3x−9 (x−4)²+(3x−9−3)²=10⇔x²−8x+16 +9x²−72x+144=10 10x²−80x+150=0 x²−8x+15=0 Δ=64−60=4

	8+2		8−2
x=		=5 lub x=		=3
	2		2

y=3*5−9=6 lub y=3*3−9=0 C₁=(5,6) lub C₂=(3,0) Najłatwiej wektorowo.

lełoś : dziękuję