Dla bezendu
5-latek: Jeszce raz to zadanie .
W trojkacie ABC (gdzie AC to podstawa ) dwusieczna kata wewnetrznego przy wierzcholku B
przecina bok AC w punkcie D . Dlugosci odcinkow AD i DC sa rowne a i b (a>b)
Przez srodek O odcinka BD poprowadzono prosta prostopadle do BD ktora przecina przedluzenie
podstawy AC w punkcie X . Mamy obliczyc dlugosc odcinka XD.
Rysunek juz zrobila Mila w poprzednim watku.
9 sie 21:55
bezendu: Ok mam już ten rysunek zaraz zaczynam działać

9 sie 22:02
5-latek: Dorysuj jeszcze ta dwusieczna kata zewnetrznego ABC i oznacz punkt przeciecia z bokiem Ac przez
Y . i daj rysunek na forum zeby wszystko bylo widac . Moze tez Saizou sie podlaczy
9 sie 22:08
5-latek: Przepraszam . Mialo byc z przedluzeniem boku AC a nie z bokiem AC
9 sie 22:12
bezendu:
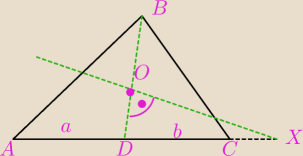 5−latek
5−latek na rysunku
Mila zaznaczyła już punkt przecięcia boku AC jako punkt D
9 sie 22:14
Saizou :
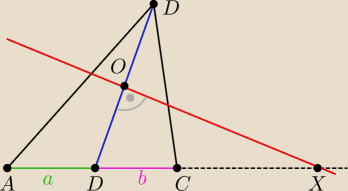
rysunek mam

9 sie 22:16
bezendu: 
9 sie 22:17
5-latek: Oczywiscie ze tak.
Wiesz co to jest kat zewnetrzny . Pokaz kat zewnetrzny przy wierzcholku B na tym rysunku
9 sie 22:17
Saizou : od góry ma być wierzchołek B

9 sie 22:17
bezendu:

9 sie 22:20
5-latek: . Bezendu . Podaj definicjre kata zewnetrznego trojkata ,.
9 sie 22:25
bezendu:
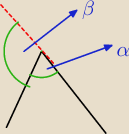
α+β=180
0
9 sie 22:27
5-latek: Czyli inaczej mowiac jest to kat przylegly do kata wewnetrznego.
Tylko na rysunku poprowadz go z drugiej strony i dwusieczna tego kata ma przeciac przedluzenie
boku AC w punkcie Y
9 sie 22:32
5-latek: Bedzie to nam potrzebne do napisania odpowiednich proporcji ale to juz wyjdzie w trakcie
rozwiazania
9 sie 22:34
Mila:
To bardzo ładne zadanie.

9 sie 22:36
bezendu:
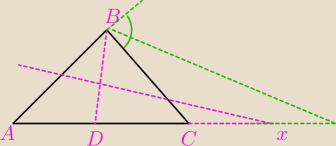
tak ?
9 sie 22:36
5-latek: No gitara tylko pamietaj tez o pozostalych oznaczeniach i zaznacz punkt Y
Wspominalem CI wczoraj o tym bys sobie przypomnial te twierdzenia .
teraz nalezy je zastosowac .
9 sie 22:40
bezendu: hmm ale od czego tu zacząć ?
9 sie 22:48
5-latek: Podpowiedz. Skorzystaj teraz z rwierdzienia o dwusiecznej kata wewnetrznego trojkata i napisz
| | AD | |
czemu jest rowny stosunek |
| |
| | DC | |
9 sie 22:49
bezendu: szczerze mówiąc to nie wiem

9 sie 22:51
5-latek: To jeszce raz przeczytaj to twierdzenie .

9 sie 22:54
bezendu: Czytam ale ale dla mnie to wygląda tak jeśli odciek AB=x AD=a BC=y DC=b
9 sie 22:58
5-latek: | | a | |
Jesli juz wezniemy Twoje oznaczenia to |
| ={x}{y} |
| | b | |
| | AD | | AB | |
To mozemy zapisac ze |
| = |
| |
| | DC | | BC | |
Teraz skorzystaj z twierdzenia o dwusiecznej kata zewnetrznego i napisz czemu jest rowny
| | AD | | AB | |
stosunek |
| = |
| =...... z rysunku |
| | DC | | BC | |
9 sie 23:07
bezendu: Może jakaś podpowiedź ?
9 sie 23:10
5-latek: Twierdzenie .
Jesli dwusieczna kata zewnetrznego trojkata przecina przedluzenie boku przeciwleglego to
odcinki ograniczone tym punktem przeciecia i koncami tego boku sa proporcjonalne do
przyleglych bokow trojkata.
9 sie 23:16
bezendu: dziś i tak już nic nie wymyśle muszę jutro poczytać jeszcze i przeanalizować ostatnie zadanie
bo też nie do końca je rozumiem..
9 sie 23:20
5-latek: No dobrze. Patrz uwaznie na rysunek i to twierdzenie
| | AY | | AB | |
Mamy tak z tego twierdzenia |
| = |
| |
| | CY | | BC | |
9 sie 23:25
5-latek: Dobrze . To jutro skonczymy chyba z e
Saizou cos wymysli

9 sie 23:27
bezendu: ale godziny wieczorne ? Dobranoc

9 sie 23:28
fx: 5−latek: jak idzie nauka matematyki?

9 sie 23:34
5-latek: Czesc
fx. Przez najblizszy czas musze sobie odpuscic gdyz na budynek w ktorym mieszkam
polozyl lape inspektor nadzoru budowlanego i jest duzo zalatwiania . Mysle ze jeszcze miesiac
bedziemy mieli juz spokoj . Do tego taki upal wiec trudno sie zmobilizowac. .

Znalazlem na allegro 2 tomy Otto za 20zl razem z przesylka i po niedzieli zamowie je .
9 sie 23:44
fx: Powodzenia i rychłego załatwienia wszelkich spraw

.
10 sie 00:20
5-latek: Bezendu dokoncze CI to zadanie ale Ty je dokladnie przeanalizuj bo to jak napisala
Mila

to ladne zadanie
| | AD | | AY | | a | |
Wobec tego |
| = |
| = |
| |
| | DC | | CY | | b | |
| | AC | | AY−CY | | AY | | a | | a+b | | a−b | |
POniewaz |
| = |
| = |
| −1= |
| −1 wiec |
| = |
| skad |
| | CY | | CY | | CY | | b | | CY | | b | |
Korzystajac z twierdzenia Talesa
| | 1 | | 2ab | |
XD= |
| DY ale DY=DC+CY=b+CY= |
| |
| | 2 | | a−b | |
| | 1 | | 1 | | 2ab | | ab | |
Wobec tego XD= |
| DY= |
| * |
| = |
| |
| | 2 | | 2 | | a−b | | a−b | |
Napisz czego nie rozumiesz z poprzedniego zadania
11 sie 16:55
11 sie 17:03
bezendu:
Witaj
5−latek ostatnio właśnie analizowałem te ostatnie zadania

Czytając Twoje posty i
Saizou trochę już to zrozumiałem

11 sie 17:23
5-latek: Nie pisalem wczoraj bo nie bylo Cie na forum .
dam CI jeszce dwa zadania i moze chwatit
zadanie nr 1(latwe) W trojkacie prostokatnym miara jednego z katow ostrych jest dwa razy
mniejza od miary drugiego kata ostrego . Oblicz pole kola opisanego na tym trojkacie jezeli
obwod okregu wpisanego w ten trojkat wynosi 2pi .
Zadanie nr 2.−naprawde latwe
W trojkacie rownoramiennym dlugosc wysokosci jest rowna h zas miara kata przy wiercholku wynosi
2 alfa . Oblicz promien okregu opisanego na tym trojkacie .
Oczywiscie rysunki ulatwia bardzo zycie
11 sie 17:48
5-latek: Tu masz latwe ale tez probuj tamte zdania co dala Eta
11 sie 17:50
Eta:
Zad.2 −−−− "długość wysokości" .... której ?
11 sie 18:02
5-latek: Opuszconej z wierzcholka na podstawe. trojkata

11 sie 18:05
bezendu: Dziękuje za zadania, postaram się zrobić

11 sie 18:18
5-latek: Do zadania nr2. Kat 2α to kat miedzy ramionami trojkata
11 sie 18:19
5-latek: Bezendu dawaj 1 zadanie z rysunkiem

11 sie 18:45
bezendu:
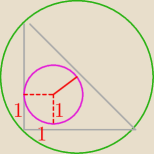
L
okegu wpisanego=2π
L=2πr=2π
r=1
P=4π
11 sie 18:56
5-latek: Ale we wzorze na pole kola jest Pk=πR2 tutaj wiec gdzie masz wyliczony proniem kola R
opisanego na trojkacie ?
Moze najpierw wylicz katy tego trojkat i skorzystaj z wlasnosci tego trojkata do ploczenia
obwodu
11 sie 19:07
5-latek: i porob oznaczenia
11 sie 19:08
5-latek: Oznacz boki trojkata , Oznacz promien R kola opisanego na trojkacie i promien r okregu
wpisanego w trojkat
11 sie 19:16
5-latek: i katy.
11 sie 19:18
bezendu:
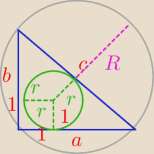
L
koła wpisanego =2π
2πr=2π
więc promień koła wpisanego r=1
11 sie 19:20
5-latek: Dobrze . Przyda sie to mam do policzenia pola trojkata . Skorzystamy ze wzoru S=p*r
Brakuje mam jeszcze do obliczenia pola trojkata niewidomej p (gdzie p to polowa obwodu)
Zeby policzyc obwod musisz policzyc ile sa rowna boki trojkata
Wiemy ze promien kola opisanego na trojkacie prostokatnym jest rowny polowie
przeciwprostokatnej wiec bok c=2R . Przeczytaj dobrze zadanie i policz bok a i b
11 sie 19:31
5-latek: bezendu podpowiedz . jest to wiedza z gimnazjum
11 sie 19:34
bezendu: Dziękuje za podpowiedź

11 sie 19:34
5-latek: I jeszce prosilem zebys oznaczyl katy ostre , Jeden kat przez α a drugi kat ostry przez 2α bo
musimy wiedziec ktory bok naprzeciwka jakiego kata lezy
11 sie 19:39
5-latek: Bezendu . Ile wynosi suma katow ostrych w trojkacie prostokatnym ? Wiec jesli namasz jeden kat
α a drugi kat 2α bo w zadaniu jest podane ze jeden kat jest dwa razy mniejszy od drugiego to
ile wynosza katy ostre tego trojkata
11 sie 19:41
bezendu:
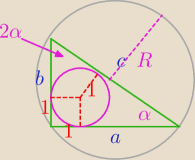
11 sie 19:43
bezendu:
300 i 600
11 sie 19:44
5-latek: Bardzo dobrze No to wedlug Twojego teraz rysnku kat α=30stopni i kat 2α=60stopni.
No to teraz jesli bok c=2R to ile rowna sie bok a i rowniez bok b wykorzystaj wlasnosc tego
trojkata
11 sie 19:49
11 sie 20:03
5-latek: Pomoge .
W trojkacie prostokatnym o katach 30,60 90 przyprostokatna lezaca naprzeciwko kata 30 stopni
| | 1 | | c√3 | |
= |
| c natomiast przyprostokatna lezaca naprzecie kata 30 stopni na dlugosc |
| |
| | 2 | | 2 | |
| | 1 | | 1 | | c√3 | | 2R√3 | |
Wiec bok b= |
| *c= |
| *2R=R , natomiast bok a= |
| = |
| =R√3 |
| | 2 | | 2 | | 2 | | 2 | |
| | 1 | | 1 | |
wobec tego p= |
| (a+b+c)= |
| (R√3+R+2R} |
| | 2 | | 2 | |
Wobec tego pole trojkata P
tr=p*r ale r=1 wiec P
tr=p
| | 1 | | 1 | |
Ale pole trojkata = sie tez Ptr= |
| a*b= |
| (R√3*R) wiec mozemy zapisac ze |
| | 2 | | 2 | |
| 1 | | 1 | |
| (R√3+r+2R)= |
| (R√3*R) wylicz z tego R i podstaw do wzoru na pole kola |
| 2 | | 2 | |
11 sie 20:13
5-latek: Nie widzialem twojego wpisu

Tam w nawiasie na koncu ma byc R zamiast r
11 sie 20:15
bezendu:
Gdzie ma być to małe r ?
11 sie 20:39
5-latek: | | 1 | | 1 | |
Ma byc tak |
| (R√3+R+2R)= |
| (R*R√3 i dalej juz dobrze |
| | 2 | | 2 | |
11 sie 20:43
5-latek: R=√3+1 wiec Pkop=πR2=π(√3+1)2=2π(2+√3)
11 sie 22:11
5-latek: Jutro drugie zadanie − do tego zadania przypomniec sobie twierdzenie o kacie srodkowym i
wpisanym

11 sie 22:13
bezendu:
5−latek zrobiłem to zadanie ale od wczoraj internet mi się rozłącza i dlatego tak wolno
odpisuje i również z tego powodu nie było mnie wczoraj

11 sie 22:21
5-latek: I czy wyniik wyszedl taki sam jak na poczatku podales? A w ogole czy bylo trudne ?nie bylo.

11 sie 22:32
bezendu:
Trochę było ja raczej staram się stopniować trudność tak jak radziła
Mila wypisałem sobie
wszystkie własności i wzory i robię teraz po kolej zadania od
Jakuba 
11 sie 22:40

 5−latek na rysunku Mila zaznaczyła już punkt przecięcia boku AC jako punkt D
5−latek na rysunku Mila zaznaczyła już punkt przecięcia boku AC jako punkt D
 rysunek mam
rysunek mam 



 α+β=1800
α+β=1800

 tak ?
tak ?





 Znalazlem na allegro 2 tomy Otto za 20zl razem z przesylka i po niedzieli zamowie je .
Znalazlem na allegro 2 tomy Otto za 20zl razem z przesylka i po niedzieli zamowie je .
 .
.
 to ladne zadanie
to ladne zadanie
 Czytając Twoje posty i
Saizou trochę już to zrozumiałem
Czytając Twoje posty i
Saizou trochę już to zrozumiałem 



 Lokegu wpisanego=2π
L=2πr=2π
r=1
P=4π
Lokegu wpisanego=2π
L=2πr=2π
r=1
P=4π
 Lkoła wpisanego =2π
2πr=2π
Lkoła wpisanego =2π
2πr=2π


 Tam w nawiasie na koncu ma byc R zamiast r
Tam w nawiasie na koncu ma byc R zamiast r



