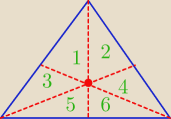
planimetria bezendu: wykaż, że 3 środkowe trójkąta dzielą go na 6 części o równych polach P_Δ5=P_Δ6 P_Δ2=P_Δ4 P_Δ1=P_Δ3 i teraz zgodnie ze symetralnymi ( symetralna dzieli trójkąt na dwa takie same trójkąty) P_Δ1+P_Δ3+P_Δ5=P_Δ2+P_Δ4+P_Δ6 P_Δ1+P_Δ2+P_Δ3=P_Δ4+P_Δ5+P_Δ6 P_Δ1+P_Δ2+P_Δ4=P_Δ3+P_Δ5+P_Δ6 P_Δ3+P_Δ3+P_Δ5=P_Δ4+P_Δ4+P_Δ5 2P_Δ3=2P_Δ4 P_Δ3=P_Δ4 P_Δ3+P_Δ2+P_Δ2=P_Δ3+P_Δ6+P_Δ6 2P_Δ2=2P_Δ6 P_Δ2=P_Δ6 P_Δ1=P_Δ3=P_Δ4=P_Δ2=P_Δ6=P_Δ5 Czy zadanie zrobione prawidłowo ? Może jakiś inny sposób? przepraszam za ten nawias ale głośno myślę

Mila: Napisz treść zadania, raz piszesz środkowe, potem symetralne, jaki trójkąt?

bezendu: polecenie napisałem wykaż, że trzy środkowe trójkąta dzielą go na sześć części o równych polach a tam oczywiście mój błąd w tym nawiasie przepraszam

duo: https://matematykaszkolna.pl/forum/205212.html

bezendu: zgadza się robiłem kiedyś to zadanie ale zapomniałem o nim już a teraz powtarzając planimetrie znowu je spotkałem a moje rozwiązanie jest ok ?

Mila: Dobrze. Popatrz na poprzednie rozwiązania. Zapamiętaj co ETA napisała na czerwono