maturalne matura : Witam Basia pomogłabyś mi w kilku zadaniach ?

wredulus_pospolitus: wrzucaj ... coś na nie poradzimy

5-latek: Artur . prosze spojrz na moj post z godziny 19.53 https://matematykaszkolna.pl/forum/208691.html

matura :

	n(n−3)
liczba przekątnych n−kata wypukłego jest równa		(n≥3) Oblicz , które wielokąty mają
	2

mniej niż 20 przekątnych

n(n−3)
	<20 /2
2

n(n−3)<40 n²−3n−40<0 Δ=169 √Δ=13

	3−13
n1=		=−5
	2

	3+13
n2=		=8
	2

ale wzór jest określony dla n≥3 3,4,5,6,7 odpowiedź dla 5 ?

ICSP: Pytanie to które wielokąty a nie ile wielokątów

matura : trójkąt, czworokąt, pięciokąt, sześciokąt, siedmiokąt ?

ICSP: na to wychodzi

matura : suma długości przyprostokątnych trójkąta prostokątnego jest równa 27, długość przeciwprostokątnej jest równa √377 oblicz pole tego trójkąta a+b=27 a²+b²=c² (27−b)²+b²=(√377)² 729−54b+b²+b²=377 2b²−54b+352=0 /2 b²−27b+176=0 Δ=25 √Δ=5

	27−5
b1=		=11
	2

	27+5
b2=		=16
	2

więc a będzie równe a=27−11=16 lub a=27−16=11 więc pole

	1
P=		ah
	2

	1
P=		*11*16=88 ok ?
	2

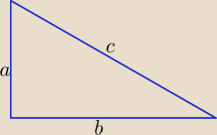
Bogdan: albo:

	1
Pole P =		ab /*4 ⇒ 4P = 2ab
	2

a² + b² = c² = 377 i a + b = 27 /² ⇒ a² + 2ab + b² = 729 ⇒ 4P = 729 − 377 = 352 P = 88

matura : Z miejscowości A do miasta B odległej od A o 600 km wyruszył samochód, Gdyby jechał z prędkością 0 10 km/h większą to przyjechałby ba miejsce w czasie 50 minut krótszym. Oblicz średnią prędkość samochodu i czas w jakim dotarł do miasta B proszę o jakieś wskazówki nie chcę gotowego rozwiązania

Bogdan: Wskazówka: Ułóż układ równań z niewiadomymi: średnia prędkość v > 0 i czas t > 0

matura : S=600 v−10

	5
t=		h
	6

	s
v=
	t

	600
(v−10)=		ok ?
	5   h 6

Bogdan: Można prawie bez ułamków:

	5
(*) vt = 600 i (**) (v + 10)(t −		) = 600
	6

	5		50		6
600 −		v + 10t −		= 600 /*		⇒ v = 12t − 10
	6		6		5

(*) (12t − 10)*t = 600 itd.

matura : czyli pierwszy warunek s=vt ?

Bogdan:

	5
Jeśli samochód zwiększa prędkość, to v + 10 i przy tym skraca czas, to t −
	6

matura : czyli mam tak w układzie równań vt=600

	5
(v+10)(t−		)=600 ?
	6

Bogdan: Tak, podałem już ten układ. Wygodnie jest najpierw przekształcić równanie drugie, które oznaczyłem (**)

matura :

	5
ok (v−10)(t−		=600
	6

(12t−10)*t=600 12t²−10t=600 6t²−5t−300=0 √Δ=85

	5−85		20
t1=		=−		odrzucam
	12		3

	5+85		15
t2=		=
	12		2

	S		600
v=		=		=80 km/h ?
	t		7,5

Bogdan: Ok.

	15
v = 12t − 10 ⇒ v = 12*		− 10 = 80
	2

To bardzo popularny typ zadań i pojawia się prawie na każdej maturze i maturze próbnej, nazywam ten rodzaj zadań: "zadanie z gdyby"

matura : właśnie dlatego chcę je dobrze opanować czyli reasumując jak mam podane jakieś tam dane to w pierwszej linijce wzór a w drugiej te minus cos plus coś ?

Bogdan: Tak. Spróbujmy jeszcze raz. To jest zadanie z matury poprawkowej z sierpnia 2012 r. Kolarz pokonał trasę 114 km. Gdyby jechał ze średnią prędkością mniejszą o 9,5 km/h, to pokonałby tę trasę w czasie o 2 godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

matura : ok vt=114 (v−9,5)(t+2)=114 dobrze układ ?

Bogdan: Dobrze. Z drugiego równania wyznacz t i wstaw do pierwszego równania, ponieważ polecenie dotyczy v, a nie t.

matura : vt+2v−9,5t−19=114 vt+2v−9,5t=133 −9,5t=133−vt−2t 9,5t=−133+vt+2t ale jak dalej ?

Bogdan:

	19
(*) vt = 114 (114 = 19*6) i (**) (v −		)(t + 2) = 114
	2

	19		19		2		4
(**) 114 + 2v −		t − 19 = 114 ⇒		t = 2v − 19 /*		⇒ t =		v − 2
	2		2		19		19

	4
(*)		v2 − 2v − 114 = 0 i v > 0,
	19

Δ = ..., itd.

matura : a jesli miałbym taki zapis jak mój post 19:38 to da się to przekształcić ?

Bogdan: Da się, ale szkoda czasu, każda chwila podczas egzaminu jest cenna. Twój kierunek rozwiązywania jest czasochłonny i łatwo w nim o popełnienie błędu.

matura : vt+2v−9,5t−19=114 114+2v−9,5t−19=114 −9,5t=19−2v 9,5t=2v−19

	4
t=		−2
	19

już zrozumiałem Δ=100 √Δ=10

	2−10
t1=		=−19
	8   19

	2+10
t2=		=28,5
	8   19

	114
v=		=4 km/h ?
	28,5

Bogdan: Masz błędne zapisy. Podaję pełne rozwiązanie.

	19
(*) vt = 114 (114 = 19*6) i (**) (v −		)(t + 2) = 114
	2

	19		19		2		4
(**) 114 + 2v −		t − 19 = 114 ⇒		t = 2v − 19 /*		⇒ t =		v − 2
	2		2		19		19

	4
(*)		v2 − 2v − 114 = 0 i v > 0,
	19

	2 − 10
Δ = 100, v =		< 0 sprzeczność
	8     19

	2 + 10		19		57
lub v =		*		=		= 28,5
	8     19		19		2

matura: ok dziękuje