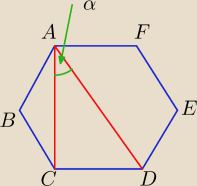
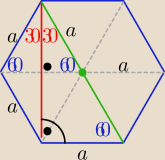
Planimetria bezendu: Oblicz miarę kąta α jakie tworzą przekątne AC i AD w sześciokącie foremnym α=30 ⁰ czy wynik się zgadza ?

Lorak: Zgadza się.

max: Chodziłeś do gimnazjum ?

bezendu: Nie ale chciałem się upewnić, a planimetrię robię od początku, więc może być więcej takich pytań

5-latek: Max . Chodzilem do 8−letniej szkoly

max: A ja .........tylko do 7− letniej Pozdrawiam "małolatku"

5-latek: bezendu Zadanie nr 1. Odcinek AB o dlugosci 14,4 cm podzielony zostal na odcinki AC CD i DB ktorych dlugosci tworza stosunek 2:6:8 . Oblicz odleglosc pomiedzy srodkami odcinkow AC i DB

bezendu:

	9
AC=
	5

	27
CD=
	5

	36
DB=
	5

9		27		18
	+		+		=9,9
10		5		5

5-latek: Zadanie nr 2.. Co to sa katy wierzcholkowe. ,oraz udowodnij ze katy wierzcholkowe sa rowne . Zrob rysunek do dowodu. zadanie nr 3. Z pewnego punktu A lezacego na okregu wyprowadzono dwie rownwe cieciwy AB i AC . poczym punkty A,B,C poloczono z esrodkiem okregu. . Udowodnij z etrojkaty AOBi AOC sa przystajace. Wskazowka . Skorzystaj z jednej 3 cech przystawania trojkatow. Zadanie nr 4 −latwe. Podstawa trojakta rownoraniennego jest rowna 10. a obwod trojkata =40. OBlicz dlugosci ramion

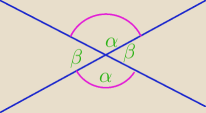
bezendu: zadanie 2 kąt α i β są to kąty przyległe więc muszą tworzyć kat 180⁰ więc 2α+2β=360

5-latek: A tak poza tym w nawiazaniu do twojego postu z 18.47. Pytanie . CO nazywamy odcinkiem. Czy rysunek wobec tego jest prawidlowy ?

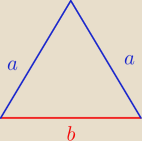
bezendu: zadanie 4 2a+b=40 2a=40−b 2a=40−10 2a=30 a=15 więc ramiona mają długość 15

bezendu: odcinek ma początek i koniec powinny być jeszcze dwie kreski jedna na początku a druga na końcu

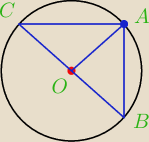
bezendu: cecha bbb ?

wredulus_pospolitus: niby tak ... pod warunkiem że nasz napisane że AO to wysokość trójkąta ABC wtedy też może być cecha kbb, a nawet kkb

5-latek: tak masz skorzytac z tej cechy. A nad dowodem o katach wierzcholkowych jeszcze raz sie zastanow bo to co napisales nie jest dowod na to z ekaty wierzcholkowe sa rone .

bezendu: α₁+β₁=180⁰ α₁=α₂ α₂+β₁=180⁰ β₁=β₂ β₁=180⁰−α₁ (z pierwszego równania ) β₁=180⁰−α₂ ( z drugiego równania) teraz ok ?

bezendu:

5-latek: Zauwaz ze kat β₂wraz z katem α₁ tworza kat polpelny wiec kat β₂=180−kat α₁. Podobnie kat β₁ z katem α₁ sa katami przyleglymi wiec kat β₁=180−kat α₁. Z tych dwoch rownosci wynika wiec ze kat β₂=katowi β₁ Udowodnilismy nastepujaca prawde geometryczna. Katy wierzcholkowe sa sobie rowne >

bezendu: a w moim dowodzie co jest nie tak ?

5-latek: Zadanie . W trojkacie rownobocznym ABC (gdzie A to wierzcholek gorny, B−wierzcholeek dolny lewy i C−wirzcholek dolny prawy ) odcinek AD jest dwusieczna kata BAC zas odcinek AE dzieli na polowe kat DAB a odcinek AF dzieli na polowe kat DAC . Udowodnij z e odcinki AE i AF sa rowne

bezendu: a odpowiedź na moje pytanie post 20:11 ?

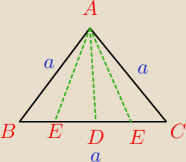
bezendu: dwusieczna w trójkącie równobocznym zawarta jest w jego symetralnej czyli dzieli bok AC na połowę dając dwa trójkąty prostokątne a dalej hmm ?

bezendu: dzieli bok BC na połowę (poprawka)

5-latek: Dwusiecna dzieli bok BC na polowe i tam ma byc miedzy DC F a nie E Rozpatrz trojkaty DAE i DAF i zastanow sie czy sa przystajace .Jesli tak to na podstawie jakiej cechy

bezendu: te trójkąty są przystające na podstawie b−k−b

bezendu: 5−latek ale nadal zastanawia mnie zadanie z tymi kątami wierzchołkowymi ?

5-latek: To za malo . Ty masz wykazac ze te trojkaty sa przystajace wobec tego ich elementy sa rowne . Moze rozpatrz inna ceche kbk

bezendu: ta cecha też jest ok ale jeśli dwusieczna AD dzieli kąt na połowę a tam jest trójkąt równoboczny więc mamy po 30⁰ ( przy wierzchołku) a przy podstawię jeśli dwusieczna zawarta jest w symetralnej czyli pada na bok BC pod kątem prostym czyli kąty przy podstawie 90⁰ i 60 stopni więc pasuję też cecha kkk więc te trójkąty są podobne czyli AF=AE teraz ok ?

5-latek: DObrze , ale mozesz tez wziac ceche kbk bo 1. Bok AD jest wspolny 2. kat DAE=katowi DAF dlatego ze kazdy z tych katow stanowi 1/4 kata BAC 3. Kat ADE=katowi ADF jako katy proste

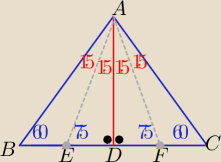
max: trójkąt AEF jest równoramienny o ramionach |AE|=|AF| ..... koniec dowodu @ 5−latka ........co Ty za zadania wymyślasz( dla przedszkolaków?

bezendu: Eta a no racja bo jak było 60 to dwusieczna 30⁰ i 15 ⁰ stopni jest przy wierzchołku zadania bardzo fajne na głęboką wodę się na razie nie rzucam

max:

bezendu: a zobacz to zadanie a kątami wierzchołkowymi mój post 19:47 ?

5-latek: Eta nie bede mu dawal trudnych na poczatek bo pisal ze zaczyna . Na trudniejsze przyjdzie pora https://matematykaszkolna.pl/forum/208548.html zobacz tam dalem zadania z planimetrii i zobacz co odpisal bezendu dalem rowniez takie zadania tylko nie pamietam w ktorym linku Zadanie . W plaszcyznie trojkata rownobocznego ABC o boku dlugosci a znalezc pole obszaru zawierajacego takie i tylko takie punkty M ze a) katy AMB BMC CMA sa rozwarte b) katy AMB i BMC sa zawatrte w predziale <60;90stopni> Pozdrawiam i

5-latek: Nastepne . jesli chcesz. W pewnym czworokacie ABCD dane sa jego przekatne AC=18cm i BD=20cm . Srodki bokow tego czworokata polaczono kolejno odcinkami i otrzymano nowy czworokat KLMN . Oblicz obwod tego tego czworokata i udowodnij ze nowo otrzymany czworokat jest rownoleglobokiem

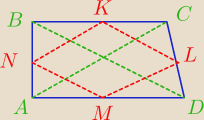
bezendu: hmm ?

5-latek: Jesli wezniesz pod uwage trojkat ABC co co wiesz o odcinku NK ?

5-latek: To samo jesli wezniesz pod uwage trojkat ADC to co powiesz o odcinku ML

bezendu: odcinek NK jest równoległy do odcinak AC

5-latek: tak zgadza sie . A ile jest rowny. Wykorzystaj twierdzenie o linii srdkowej trojkata Zauwaz ze odcinek NK laczy srodki bokow BA i BC a dalej to juz pryszcz

bezendu: o linii środkowej trójkąta ?

5-latek: Znasz to twierdzenie ? Mowi ono ze: Odcinek laczacy srodki dwoch dowolnych bokow trojkata jest rownolegly do trzeciego boku i rowny jego polowie >

bezendu: nie znam, na stronce nie było tego

Godzio: A to akurat jest ważne twierdzenie, warte zapamiętania (na mojej maturze musiałem z niego skorzystać )

5-latek: NO to teraz juz znasz i zapamietaj wiec licz ile jest rowny odcinek Mk i ML a takze odcinek NMi KL bo masz policzyc obwod i nie zapomnij udowodnic ze czwworokat KLNM jest rownoleglobokiem −To CI wyjdzie z zadania Wiec wysnuj odpowiedni wnisek

5-latek: Czesc Godzio

bezendu: NK=9 KL=10 ML=9 NM=10 Obw=38 Witaj Godzio ,a jak dokładnie nazywa się to twierdzenie ?

5-latek: Obwod dobrze ale jeszcze masz wykazac ze jest rownoleglobokiem

5-latek: http://www.google.pl/url?sa=t&rct=j&q=twierdzenie%20o%20linii%20%C5%9Brodkowej%20w%20tr%C3%B3jk%C4%85cie&source=web&cd=1&cad=rja&ved=0CCoQFjAA&url=http%3A%2F%2Fpl.wikipedia.org%2Fwiki%2FLinia_%25C5%259Brodkowa&ei=8O7_UZ-sFsHStQaD_YHICg&usg=AFQjCNGJ5jP0mFa5KNIvDwuHv2fGHbUKOg zobacz tutaj

bezendu: o linii środkowej słyszałem ale tylko w trapezie hmm ma dwie pary boków które są do siebie równoległe i tej samej długości

5-latek: OK. Stwierdzilismy ze odcinki Nk i ML sa rownolegle do AC wiec sa do siebie rownolegle a ze sa sobie rowne wiec ten czworokat jest rownoleglobokiem czyli mozemy wysnuc taki wnniosek. Jezeli w dowolnym czworakacie polaczymy kolejno srodki jesgo bokow otrzymamy rownoleglobok]] bezendu dzisiaj juz wystarczy bo jestem zmeczony . Bede tylko przegladal linki . Jutro moze tez jakies ciekawe zadania znajde . Czesc}

bezendu: Dziękuje za zadanie i wytłumaczenie to dużo mi daję Miłego wieczoru i do zobaczenia jutro