zadania Eta: Zadania .... dla chętnych ( przyszłych maturzystów zad.1/ Liczby dodatnie x, y spełniają warunek:

	x+y
		= √xy+3
	2

Wykaż,że co najmniej jedna z nich jest liczbą niewymierną zad.2/ Wykaż,że dla każdych dodatnich liczb a,b ∊(0,1) zachodzi nierówność a√b+b√a +1>3ab zad.3/ Dany jest trapez równoramienny ABCD , AB II CD , |AB| >|CD| i |BC|>|CD| Kąty rozwarte tego trapezu mają miarę 120^o. Na ramieniu AD wybrano taki punkt M,że |AM|=|DC| Wykaż,że |BM|=|AC|

ICSP: Jako że postanowiłem poprawiać maturę te zadanka również są dla mnie

Saizou : zadanie nr. 1

x+y
	=√xy+3 /2 bo L i P>0
2

x2+2xy+y2
	=xy+3
4

x²+2xy+y²=4xy+12 x²−2xy+y²=12 (x+y)²=12 lx+yl=2√3 x+y=2√3 drugiej wersji nie rozpatruję bo x,y>0 x=2√3−y →y>2√3 →że jedna x musi być liczbą niewymierną (analogicznie dla y)

Garth: @ICSP − to jaki miales wynik i jakie sa Twoje obecne aspiracje? Czy moze chcesz poprawiac, ale nie z matematyki?

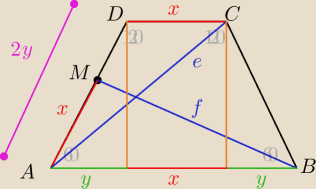
Saizou : z tw. cosinusów otrzymamy e²=(2y)²+x²−2*2y*x*cos120 cos120=cos(90+30)=−sin30

	1
e2=4y2+x2−4xy*(−		)
	2

e²=4y²+x²+2xy f²=x²+(2y+x)²−2*x*(2y+x)*cos60

	1
f2=x2+4y2−4xy+x2−2x(2y+x)*
	2

f²=2x²+4y²−4xy−2xy−x² f²=4y²+x²+2xy f²=e² →f=y, bo e,f>0

Saizou : oczywiście zrobiłem błąd w pisaniu

	1
f2=x2+4y2+4xy−2x(2y+x)*
	2

..... f²=4y²+x²+2xy

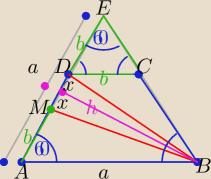
Eta: 2 sposób ( rys. ) trójkąt ABE jest równoboczny o boku dł . "a"= 2b+2x . x>0 h −−− jest jego wysokością ⇒ trójkąt BMD jest równoramienny o ramionach BM i BD |BD|= |AC| −−−− dł. przekątnych trapezu zatem: |BM|=|AC| c.n.u

Eta: zad.4/ Dane są dwa prostokąty o równych polach i równych obwodach. Wykaż,że długości przekątnych tych prostokątów są też równe.

Eta:

	a−b
zad.5/ Dodatnie liczby a i b mają tę własność,że liczba		jest wymierna.
	a+b

	5a−b
Wykaż ,że liczba		też jest liczbą wymierną.
	5a+b

Eta: Hej Saizou ......... łap zadanka

Saizou : mamy prostokąt o bokach a,b oraz d przekątną P=ab L=2(a+b)

	1
d=√a2+b2=√(a+b)2−2ab=√(		L2−2P}, z tego wynika że jeśli prostokąty mają takie
	2

same pole i obwód to ich przekątne mają taką samą długość

Saizou : coś źle zapisałem

	1
d=√		L2−2P
	4

Piotr: Ja mam nawet fajne zadanko(ostatnio je robiłem)

	π
Jaką najmniejszą wartość może przyjmować wyrażenie tgα+ctgα wiedząc, że α∊(0,		) ?
	2

Saiozu dla Ciebie

Saizou : y=tgx+ctgx

	sinx		cosx		sin2x+cos2x		1
y=		+		=		=		=
	cosx		sinx		sinxcosx		sinxcosx

1		2
	=
1   sin2x 2		sin2x

a żeby osiągnąć najmniejszą wartość to musimy dzielić przez największy mianownik

	π		2
czyli dla x=		otrzymujemy		=2
	4		1

Piotr: 2 sposób Korzystam z nierówności pomiędzy średnia arytmetyczna a średnia geometryczną:

tgα+ctgα
	≥√tgα*ctgα
2

tgα+ctgα≥2√tgα*ctgα tgα+ctgα ≥ 2 a więc najmniejsza wartość to 2

Eta: Zad 5/ ? czeka.......

Mateusz: Moze sie skusze na piąteczke

Eta: ............

Mateusz: O.oo dzieki za jabłuszko zgłodniałem dlatego chciałem sie skusic na zadanko Teraz juz go nie rusze

Piotr: Ja mam pewien pomysl na te zadanie 5 zaraz przedsawie swoje rozumowanie

Piotr: Założenie: a oraz b > 0

a−b
	=W , gdzie W to liczba wymierna
a+b

a−b		a+b−2b
	=		=1−2b=W
a+b		a+b

5a−b		5a+b−2b
	=		=1−2b
5a+b		5a+b

A wiem, że z zalożenia 1−2b jest liczba wymierną a więc

5a−b
	∊W c.n.u
5a+b

Hmm?

Piotr: juz widze bląd w ulamkach... a wiec zle

Eta: @Piotra Tu masz błąd:

5a+b−2b		2b
	= 1 −
5a+b		5a+b

Eta:

Piotr: A w dobra strone ide czy nie?

Saizou : i jeszcze wyżej

a−b		a+b−2b		2b
	=		=1−
a+b		a+b		a+b

Eta: Tak , też ten sam błąd !

Piotr: Wiem, wiem

Eta: Zapamiętaj ,że tak nie możesz dzielić bo co by to było na maturze?

Piotr: Przypał . Jakoś tak mi się ''napisało''. Za szybko chciałem

Saizou : ja miałem taki pomysł, że

	a−b		b		x−1
x=		→−		=
	a+b		a		x+1

	5a−b		1		b		y−1
y=		→		*(−		)=
	5a+b		5		a		y+1

x−1)		y−1		3x−2
	=		→y=		tylko nie wiem co dalej
5(x+1)		y+1		2x+3

Eta: myśl dalej ..........

Mateusz: Bardzo fajny i prosty dowod mozna przeprowadzic korzystając z własnosci ze kazda liczbe wymierną mozna przedstawic w postaci ułamka nieskracalnego.

Saizou :

	3		13
y=		−		i teraz już chyba widać że jest to liczba niewymierna
	2		2(2x+3)

Saizou : oczywiście miało być wymierna

Basia: a skąd wiesz, że Ci wolno dzielić przez a ?

	a−b
dla a=0 i b≠0		= −1; założenie jest spełnione
	a+b

	b
ale		nie istnieje
	a

dowód musi być kompletny

a−b
	= w ∊ W
a+b

a−b = w(a+b) a − wa = b+ wb a(1−w) = b(1+w) i mniej liczenia będzie jak wyznaczysz b, ale musisz rozważyć dwa przypadki 1. w = −1 i zapisać co się wtedy dzieje 2. w≠ −1

	a(1−w)
b =
	1+w

podstawić do drugiego i wykonać proste rachunki

Saizou : bo a,b>0

Eta: Hej Basiu w treści "Liczby dodatnie a i b".......

Basia: Hej Eto nie doczytałam; ale jak widać twierdzenie jest prawdziwe dla dowolnych a,b takich, że a+b≠0

Eta: Jasne, ale w treści .... uprościli do liczb dodatnich

Saizou : no to teraz drogie Panie, czy to 'coś ' co przedstawiłem jest przekonujące?

Basia: nie chce mi się liczyć, bo strasznie to skomplikowałeś, ale jeżeli nie ma błędu w obliczeniach to może być, chociaż można znacznie prościej

Eta: Mogłeś, dokończyć np tak:

	b		x−1		a
skoro x∊W i −		=		−− też wymierna , to i		też wymierna
	a		x+1		b

zatem:

	5a−b		a   5* −1   b
		=		−−−−−−− wymierna
	5a+b		a   5* +1   b

Godzio: Zostały jeszcze jakieś do zrobienia ?

Saizou : Godzio zadanie 2 wciąż nierozwiązane

Godzio: To przecież się samo robi a√b + b√a + 1 > 3³√a^3/2 b^3/2 * 1 = 3√ab > 3ab

Godzio: Eta następnym razem chcemy trudniejsze

ccc: Rozwiąż równanie w liczbach rzeczywistych

3

1

4

4

1

3

+

+

+

+

+

=0

x

x−1

x−2

x−3

x−4

x−5

asdf: x=2,5

ccc+: ok no to lecimy D=R\{0,1,2,3,4,5} 3(x−1)(x−2)(x−3)(x−4)(x−5)=3x⁵−45x⁴+255x³−675x²+822x−360 x(x−2)(x−3)(x−4)(x−5)=x⁵−14x⁴+71x³−154x²+120x 4x(x−1)(x−3)(x−4)(x−5)=4x⁵−52x⁴+236x³−428x²+240x 4x(x−1)(x−2)(x−4)(x−5)=4x⁵−48x⁴+196x³−312x²+160x x(x−1)(x−2)(x−3)(x−5)=x⁵−11x⁴+41x³−61x²+30x 3x(x−1)(x−2)(x−3)(x−4)=3x⁵−30x⁴+105x³−150x²+72x po oddaniu 16x⁵−200x⁴+904x³−1780x²+1444x−360

	5
x=
	2

	5−√7
x=
	2

	5+√7
x=
	2

	5−√17
x=
	2

	5+√17
x=
	2

ccc: Mało

ccc+:

ccc: Ten wpis był @asdf

ccc: dla ccc⁺

ccc: Jeszcze inny sposób (łatwiejszy) ................

ccc+: ccc+=bezendu nie mam innego

bezendu: przenieś na drugą stronę i pomnożyć na krzyż ?

ccc: No to jedno z nich jest robaczywe

bezendu: ale zadanie dobrze rozwiązane ?

ccc: Odp: poprawne ( przecież zawsze możesz sam sprawdzić

bezendu: ale nie chcę mi się tego sprawdzać miałem dopisać jeszcze miłego sprawdzania czy to wszystko jest dobrze wymnożone

ccc: Nie chce mi się sprawdzać ......... zwykłego mnożenia

bezendu:

bezendu: Etam

ccc:

ZKS: bezendu nie sądzę żebyś rozwiązał równanie 16x⁵ − 200x⁴ + 904x³ − 1780x² + 1444x − 360 = 0 więc ja bym Ci rozwiązania nie uznał.

bezendu: to już zrobił wolfram

ccc: Cffffffffaniaczek

bezendu: ale do etapu pomożenia i dodania zrobiłem sam

ccc: To teraz myśl........ nad prostszym sposobem

ccc: Na rozgrzewkę takie zadanie: Usuń niewymierność z mianownika ułamka:

6+3√2−3√6−2√3
	=......
√6−√2

Vax:

3		1		4		4		1		3
	+		+		+		+		+		= 0
x		x−1		x−2		x−3		x−4		x−5

Wystarczy zsumować 1 składnik z 6, 2 z 5 i 3 z 4, wówczas dostajemy:

3(2x−5)		2x−5		4(2x−5)
	+		+		= 0
x2−5x		x2−5x+4		x2−5x+6

	5
Jeżeli 2x−5 = 0 równość zachodzi, załóżmy, że x ≠		, dzieląc przez 2x−5 i podstawiając y
	2

= x²−5x dostajemy:

3		1		4
	+		+		= 0 ⇔ 2y2+13y+18 = 0 ⇔ (y+2)(2y+9) = 0 ⇔ (x2−5x+2)(2x2−10x+9) =
y		y+4		y+6

0 Skąd łatwo dostajemy kolejne 4 rozwiązania o których pisał ccc.

ccc: @bezendu O prostsze rozwiązanie tego równania poproś ...Vax Vax sprytniej rozwiąże ....niż wolfram

bezendu:

6+3√2−3√6−2√3		√6+√2
	*		=
√6−√2		√6+√2

	6√6+6√2+6√3+6−18−6√3−6√2−2√6
=		=
	4

4√6−12		4(√6−3)
	=		=√6−3
4		4

ccc: ......... dla Vax

ccc: @Vax i....... założenie y∊R\{0,−6,−4, }

ccc: @ bezendu 2 sposób Wystarczy wykonać zwykłe dzielenie: (6+3√2−3√6−2√3) : (√6−√2) = √6−3 −6+2√3 −−−−−−−− −3√6+3√2 3√6−3√2 −−−−−−−−−−−− = = i bingo

bezendu: wole tradycyjne metody

ccc:

bezendu: a teraz idę powtarzać planimetrię od podstaw

ccc: Mam fajne zadanko z planimetrii chcesz?

bezendu: nie

ccc:

bezendu: chyba że jest to zadanie policz pole prostokąta o bokach a= ? b=? innego nie chce

ccc: Ładny trapezik

bezendu:

bezendu: a właśnie od czego zacząć taką dobrą powtórkę z planimetrii ale chcę od podstaw bo ostatnio zadania z planimetrii liczyłem w 2 klasie

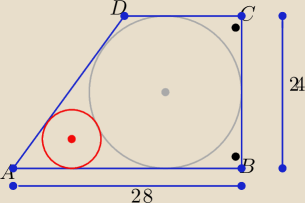
ccc: Duży i mały okrąg są styczne zewnętrznie i wszystkie dane jak na rysunku Oblicz długość promienia mniejszego okręgu

ccc: https://matematykaszkolna.pl/strona/3422.html

bezendu: Eta tam nie ma pokazanych różnych dowodów niestety

ccc: Najpierw powtórz teorię ( są też..zadania obok każdego działu

bezendu: wieczorem wpadnę i wrzucę kilka zadań chodzi o wyprowadzenie wzorów

ccc: https://matematykaszkolna.pl/strona/3349.html

ccc: @Saizou zadanie z trapezem ....... łap

Saizou : a który to nr.

Saizou : już wiem, myślałem że to jakieś zadanie z linku

5-latek: bezendu dla Ciebie z planimetrii zadanie. W trojkacie prostokatnym dwusieczna kata ostrego dzieli bok przeciwlegly temu katowi w stosunku 3:5 . Wykaz ze stosunek dlugosci promienia okregu wpisanego r w ten trojkat do dlugosci

	2
promienia okregu opisanego R na tym trojkacie jest rowny		.
	5

bezendu: 5−latek ale ja pisałem, że muszę ogarnąć podstawy jeszcze zadań na razie nie tykam dziś totalna porażka zrobiłem dwa zadania z rozszerzonej matury w ciągu 2 godzin więc dobrze nie jest

5-latek: Zadanie nr 2 . zaczynamy od podstaw. Dany jest trojkat ABC . Wiadomo ze punkt A₁ obrazem punktu A w symetrii wzgledem prostej BC a punkt B₁ obrazem punktu B w symetrii wzglem prosteij AC. Udoqwodnic ze trojkat AB₁C=trokatowi BA₁C . I moze jeszcze jedno i na razie starczy bo i tak zaraz pojawia sie inne W trojkacie ABC przez punkt O bedacy srodkiem srodkowej CC' poprowadzono prosta rownolegla do boku BC i przcinajaca boki AC i AB odpowiednio w punktach D i E Udowodnic ze stosunek

	DC
		jest jednakowy dla kazdego trojkata
	DA

bezendu: wolę już dziś nie robić żadnych zadań...

5-latek: Nie zauwazylem twojego wpisu jak pisalem nastepne ale w tym zadaniu o dwusiecznej skorzystaj z twierdzenia o dwusiecznej

5-latek: natomiast w zadaniu nr 2 skorzystaj z twierdzenia ktore mowi ze Kazda izometria jest symetria osiowa lub zlozeniem dwoch symetri osiowych lub zlozeniem trzech symetrii osiowych. rozwaz izometri bedaca zlozeniem dwoch symetrii osiowych wzldem prostej Ac i BC W trzecim skorzystaj z Twierdzenia Talesa>

5-latek : A tak poza tym to moze odpocznij pare dni chocby do konca tego tygodnia >

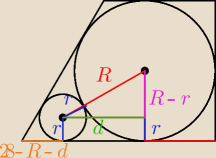
Saizou : R=12 (12+r)²=d²+(12−r)² 144+24r+r²=d²+144−24r+r² 48r=d² d=4√3r 28−R−d=28−12−4√3r=16−4√3r teraz z podobieństwa trójkątów

16−4√3r		12
	=
r		16

12r=192−64√3r 12r+64√3r=192

	192		48
r=		=
	12+64√3		3+16√3

ale coś mi tu nie pasuje

ccc: d²=48r ⇒ d=4√3r

ccc: odp: r=3 ,bo r∊(0,12)

ccc: No i co? poprawiłeś i........

ccc: taka proporcja z podobieństwa ! (nieźle namotałeś

	r		12
		=
	16−4√3r		16

to: r=12−3√3r 3√3r=12−r / ² , r€(0,12) teraz dokończ............

ccc: Dobrej nocki

Godzio: 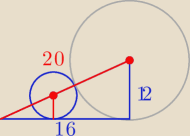√16² + 12² = 20 (przeciwprostokątna) no i zostaje proporcja:

20 − (12 + r)		r
	=		⇒ r = 3
20		12

I pytanie, dlaczego ta prosta czerwona przechodzi przez oba środki ?

ccc: No właśnie a już miałam pisać coby Saizou jak zajrzy był w

ccc: Urządził sobie wycieczkę "dookoła Świata" Pomogłam mu wyjść z tej "dżungli Amazońskiej" (tym Jego sposobem)

ccc: 111 moje Dobrego ranka Godzio

Godzio: Nie sądziłem, że jeszcze ktoś wchodzi po mnie A ja wyjątkowo teraz późnymi wieczorami, bo pracuje

Saizou : no nic nie jestem w szoku, prędzej jestem głupi że źle wyłączyłem pierwiastek, bo rozwiązać to byłby pikuś, ale cóż