zadania
max:
Zadania dla
Saizou ...
 zad.1/
zad.1/ W trójkącie o bokach długości a,b,c i obwodzie
2p
zachodzi:
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
|
| + |
| + |
| ≥2( |
| + |
| + |
| ) |
| | p−a | | p−b | | p−c | | a | | b | | c | |
zad.2/ Porównaj liczby:
a=
4√5−2√6*
√√3−√2
i
| | sin7o*sin19o+sin71o*cos367o | |
b= |
| |
| | 2sin282o | |
1 sie 23:35
ciuchcia: zad. 1 nie ma polecenia jakby nie patrząc

1 sie 23:37
max:
zad1/
wykaż 
1 sie 23:44
ciuchcia: 
1 sie 23:44
max:

1 sie 23:45
Saizou : Eto czego ty ode mnie oczekujesz o 23:46 xd
1 sie 23:46
max:
Nie napisałam,że ma być teraz rozwiązane

1 sie 23:47
bezendu: Dobry wieczór

1 sie 23:47
max:
Dobry

1 sie 23:48
max:
bezendu zobaczył zadania i............ poszedł spać?

1 sie 23:50
bezendu: Potrzebuje jeszcze czegoś z planimetrii ? jakiś ciekawy link (oprócz tego co jest na
matematyk.pisz)
1 sie 23:50
bezendu: nie poszedłem spać, walczę z planimetrią od wtorku

1 sie 23:51
max:
Powodzenia

1 sie 23:52
bezendu: Dziękuje ale słabo idzie

1 sie 23:52
Saizou : www.zadania.info xd
1 sie 23:53
bezendu: Saizou chcesz mnie zabić

najpierw muszę te zadania od Ciebie ogarnąć

1 sie 23:54
1 sie 23:55
1 sie 23:57
bezendu:
ciuchcia samobójcą nie jestem

1 sie 23:58
ciuchcia: lepiej zaczynać od trudniejszych

przy nich poznajemy podstawy
1 sie 23:59
bezendu:
ale bez sensu chyba robić zadania trudne skoro i tak ich nie ruszę jak mam braki ? nie sądzisz
?
1 sie 23:59
ciuchcia: zawsze można poprosić o hinty

2 sie 00:01
bezendu:
a nawet trzeba

2 sie 00:03
Saizou : ciuchcia takie fajne zadanka xd
2 sie 00:10
bezendu:
Saizou fajne jak ktoś śmiga z planimetrii

2 sie 00:12
Saizou : bezendu też będziesz śmigał, nawet lepiej ode mnie xd
2 sie 00:13
ciuchcia: podstawa to nie śmigać jak rządowy samolot po niebie

2 sie 00:17
Saizou : Eta w w tym drugie pierwiastku jest
√3−
√2 tak

2 sie 00:23
2 sie 00:23
bezendu: już mi się tytuł podoba a tamta już zamówiłem

2 sie 00:26
max:
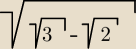
Tak
Saizou
2 sie 00:29
5-latek: W 1 czesci jest 49 lekcji .
2 sie 00:37
bezendu: 5−latek Ty posiadasz tą książkę?
2 sie 00:41
Saizou : a tam na pewno jest sin71

2 sie 00:43
Saizou : a nie dobra jest, jak zwykle nie potrafię odejmować xd
2 sie 00:44
5-latek: Tak. niedawno ja kupilem i druga czesc tez
2 sie 00:50
Saizou : a=
√4√2−3√3≈0,679
2 sie 00:57
Godzio: a =
√3 −
√2
i teraz pokaż, że a > b, przybliżenie to nie dowód

2 sie 01:54
Saizou : Godzio ale mam tylko porównać liczby

nie pisze w jaki sposób
2 sie 02:06
Godzio:
Skoro masz porównać to masz dowieźć, że któraś z nich jest większa

A napisanie, że ta jest większa bo ≈ ... to wiesz

2 sie 02:13
max:
Zjadłeś
Saizou minusa

2 sie 12:54
max:
Przed maturą ... zjedz


2 sie 12:55
max:
Wykaż,bez użycia
kalkulatora 
2 sie 12:56
Godzio:
No skoro tam jest minus to już nie ma czego dowodzić

2 sie 13:02
Saizou : no to może tak
zakładam że to prawda
2 sie 13:06
Godzio:
No, i to jest dowód

2 sie 13:07
Godzio:
Tylko jeszcze taki znaczek "⇔" jest potrzebny pomiędzy każdym przejściem

2 sie 13:08
Saizou : sin7*sin19+sin71*cos367=sin7*sin19+cos19*cos7=cos(19−7)=cos12
2sin282=2sin(270+12)=2cos12
tylko gdzie?
2 sie 13:08
Godzio:
A sinus jest dodatni czy ujemny w IV ćwiartce

?
2 sie 13:09
Saizou : ujemny xd, za bardzo się wkręciłem z zamianą na kofunkcję i wyszło że podałem dla cosinusa
zamiast dla sinusa
2 sie 13:10
Godzio:
No dobra, teraz 1 zadanie

Też się nad nim pomęczę
2 sie 13:12
Godzio:
Przyjemne zadanie

2 sie 13:16
max:

2 sie 20:21
Saizou : na razie nie mam jakoś pomysłu na to, ale coś kiedyś wymyślę
2 sie 23:17
colo: Mógłby ktoś rozwiązać pierwsze zadanko dla Saizou?
2 sie 23:44
Saizou : proszę mi nie tykać tego zadanka xd (oczywiście żart)
muszę jeszcze posiedzieć nad nim

2 sie 23:45
max:
Na razie nie .... poczekamy do końca wakacji

2 sie 23:46
colo: A chociaż jakaś wskazówka?
3 sie 00:03
Saizou : można by spróbować od pokazania że
3 sie 00:20
max:
Zastosuj podstawienie dla x, y,z >0
a= x+y , b= x+z , c= y+z
2p=......
3 sie 00:23
Saizou : bo ja tak jak zacząłem liczyć to moje to wyszło mi 2a≥b+c
3 sie 00:26
max:
kontynuuję:
2p= x+y+x+z+y+z ⇒ p= x+y+z
:
:
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
to do wykazania |
| + |
| + |
| ≥ 2( |
| + |
| + |
| ) |
| | x | | y | | z | | x+y | | x+z | | y+z | |
z nierówności między średnimi am− hm
:
:
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
2*( |
| + |
| + |
| )≥4( |
| + |
| + |
| ) |
| | x | | y | | z | | x+y | | x+z | | y+z | |
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
|
| + |
| + |
| ≥2( |
| + |
| + |
| ) |
| | x | | y | | z | | x+y | | x+z | | y+z | |
co......... kończy dowód

3 sie 00:43
bezendu: Eta proszona do mojego wątku o planimetrii

zadałem tam pytanie ? jak byś miła chwilkę
to zapraszam

3 sie 00:44
colo: Piękny dowód, bardzo mi się podoba i jednocześnie dziękuję

3 sie 00:52
max:


3 sie 00:56
max:
Na jutrzejszy dzień
 zad.3
zad.3 W trójkącie prostokątnym ABC wysokość poprowadzona z wierzchołka
kąta prostego podzieliła trójkąt na dwa trójkąty o obwodach
2m i
2n
Oblicz obwód trójkąta ABC
3 sie 01:11
bezendu: na jutrzejszy dzień czyli na niedzielę ?

3 sie 01:12
max:
Oj tam...

3 sie 01:13
bezendu: Możesz sprawdzić wynik do tamtego zadania zrobiłem jeszcze raz

3 sie 01:14
Godzio: 
3 sie 03:42
pigor: ..., a jak ktoś chce, to jeśli x>0, y>0 :
(x−y)2 ≥0 ⇔ x2−2xy+y2 ≥0 /+4xy ⇔ (x+y)2 ≥4xy /: xy(x+y) ⇔
⇔ x+yxy ≥ 4x+y ⇔ 1x+1y ≥ 4x+y
3 sie 11:08
max:

3 sie 18:18
Mila: Zadanie z próbnej maturki.
Liczby naturalne parzyste od 2 do 100 zapisujemy kolejno jedna za drugą tworząc liczbę
naturalną a.
Czy liczba a jest kwadratem pewnej liczby naturalnej?
3 sie 19:03
max:
Coś nikt z
maturzystów się nie rwie

......... do
zad.3/
4 sie 18:38
bezendu: Eta maturzyści dopiero od września

4 sie 18:48
max:
:

4 sie 18:49
Eta:
@
Saizou ......... zad3 .... czekaaaaaa

4 sie 21:58
Saizou : hehe to niech czeka

muszę tylko uzależnić wysokość h od m,n i będzie dobrze bo OB
ABC=2(m+n−h)
4 sie 21:59
Eta:
w tym "sęk"

4 sie 22:02
Eta:
zad.4/ W prostokącie ABCD o boku |CD|=4 , obrano punkt M będący środkiem boku AB.
Dwusieczna kąta BCD podzieliła trójkąt AMD na dwie figury o równych polach.
Oblicz długość boku |AD|.
4 sie 22:19
Technik: Widzę zmagania maturzystów

4 sie 22:23
Eta:
zad.5/ W trójkącie równoramiennym ABC, |AC|=|BC| na podstawie AB trójkąta
wybrano punkty P i Q(różne od A i B)
Z punktu P i Q poprowadzono odpowiednio odcinki m i n oraz k i w
prostopadłe do ramion tego trójkąta.
Wykaż,że m+n= k+w
4 sie 22:27
Technik:
zadanie 5 bardzo fajne

ale to nie dla maturzystów tylko dla @Saizou

4 sie 22:31
Eta:
Witaj " techniku " ..
studencie 
4 sie 22:33
Technik: Witam

odpowiedziałem Ci kiedyś w jakimś poście

na Twoje pytanie

4 sie 22:34
4 sie 22:35
Eta:

4 sie 22:36
Technik: Może za rok poprawię wynik matury jak mi się będzie chciało

4 sie 22:37
5-latek: TO moze takie zadanko nr6 i czas spac.
W okrag o promieniu R wpisano trojkat rownoramienny w ktorym suma ramienia i wysokosci
opuszczonej z wierzcholka na podstawe jest rowna m . Obliczyc wysokosc jezeli przyjmiemy R i
m za wiadome .
5 sie 00:33
Eta:
@
Saizou 
....... wciąż czekam na rozwiązanie
zad.3
5 sie 22:07
Eta:
i......
zad.4, zad.5 
5 sie 22:10
bezendu: i nr 6

5 sie 22:11
Saizou : wakacje są i trzeba się nimi trochę nacieszyć xd

5 sie 22:16
Eta:

5 sie 22:23
bezendu: 
5 sie 22:27
rownanie: To podam odpowiedź do 4 (mam nadzieje ze dobrą)

|AD|=
√33−1
6 sie 10:50
Saizou :
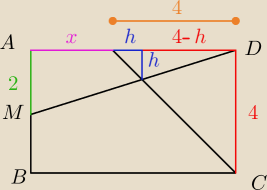
z Talesa mamy
x
2+10x−8=0
| | −10−2√33 | |
x1= |
| <0 sprzeczność |
| | 2 | |
lADl=
√33−5+4=
√33−1
6 sie 14:09
Eta:

Inny sposób:
| | 4*y | |
ponieważ z treści zad. : P1=P2 to 2*x= 4P1 i P1= |
| = 2y |
| | 2 | |
2x= 8y ⇒
x= 4y
Z podobieństwa trójkątów
| | 2 | | 4y | | −1+√33 | |
|
| = |
| ⇒ 2y2+y−4=0 y= |
| |
| | y | | 4−y | | 4 | |
to:
x=|AD|= 4y=
√33−1 [j]
6 sie 17:25
 zad.1/ W trójkącie o bokach długości a,b,c i obwodzie 2p
zachodzi:
zad.1/ W trójkącie o bokach długości a,b,c i obwodzie 2p
zachodzi:











 najpierw muszę te zadania od Ciebie ogarnąć
najpierw muszę te zadania od Ciebie ogarnąć 

 przy nich poznajemy podstawy
przy nich poznajemy podstawy






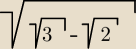 Tak Saizou
Tak Saizou


 nie pisze w jaki sposób
nie pisze w jaki sposób
 A napisanie, że ta jest większa bo ≈ ... to wiesz
A napisanie, że ta jest większa bo ≈ ... to wiesz 







 ?
?
 Też się nad nim pomęczę
Też się nad nim pomęczę





 zadałem tam pytanie ? jak byś miła chwilkę
to zapraszam
zadałem tam pytanie ? jak byś miła chwilkę
to zapraszam 



 zad.3 W trójkącie prostokątnym ABC wysokość poprowadzona z wierzchołka
kąta prostego podzieliła trójkąt na dwa trójkąty o obwodach 2m i 2n
Oblicz obwód trójkąta ABC
zad.3 W trójkącie prostokątnym ABC wysokość poprowadzona z wierzchołka
kąta prostego podzieliła trójkąt na dwa trójkąty o obwodach 2m i 2n
Oblicz obwód trójkąta ABC





 ......... do zad.3/
......... do zad.3/



 muszę tylko uzależnić wysokość h od m,n i będzie dobrze bo OBABC=2(m+n−h)
muszę tylko uzależnić wysokość h od m,n i będzie dobrze bo OBABC=2(m+n−h)


 ale to nie dla maturzystów tylko dla @Saizou
ale to nie dla maturzystów tylko dla @Saizou 

 odpowiedziałem Ci kiedyś w jakimś poście
odpowiedziałem Ci kiedyś w jakimś poście  na Twoje pytanie
na Twoje pytanie 



 ....... wciąż czekam na rozwiązanie zad.3
....... wciąż czekam na rozwiązanie zad.3





 |AD|=√33−1
|AD|=√33−1

 Inny sposób:
Inny sposób: