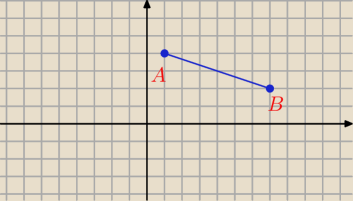
Geometria analityczna bezendu: Dany jest trójkąt równoramienny ABC o kącie prostym przy wierzchołku C i wierzchołkach A=(1.4) B=(7,2) Wyznacz współrzędne wierzchołka C tego trójkąta Można jakąś wskazówkę ?

Patryk: iloczyn współczynników kierunkowych prostych AC I BC musi być równy −1

bezendu: ok dzięki

Patryk: dalej musisz ulżyć jakieś warunki,pewnie wiesz, i pokombinowac

bezendu: już jestem w połowie zadania

Saizou : np. −obliczyć pole trójkąta ABC −obliczyć długość wysokości opuszczonej z wierzchołka C −wysokość jest równa długości odcinka CS, gdzie S to środek AB − żeby wszytko uzależnić od jednej niewiadomej wyznaczasz prostą prostopadłą do AB przechodzącą przez punkt S

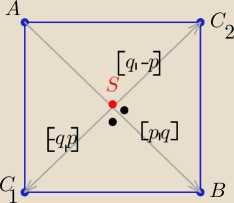
ccc: Najprościej z wykorzystaniem wektorów

	7+1		4+2
S(		,		)= (4, 3)
	2		2

Odpowiednie wektory są równe i prostopadłe ( w kwadracie) → BS= [3,−1]= [p,q] to: C₁S= [4−x, 3−y]= [−q, p]= [1,3] ⇒ 4−x=1 i 3−y=3 ⇒ x=3 i y=0 ... C₁(3,0) C₂S=[q, −p]= [−1,−3] ⇒ 4−x=−1 i 3−y= −3 ⇒ x=5 i y=6 ... C₂(5,6)

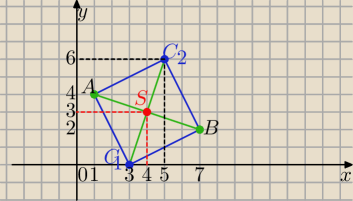
ccc: No i widać ....... wszystko gra

Kostek: Dziękuje za wskazówki ale wystarczyła podpowiedź Patryka

bezendu:

bezendu: Eta masz chwilkę czasu jeszcze ?

ccc: Jakby się ktoś chciał "przyczepić" to należało napisać wektory (na pierwszym rys. ) SB i SC₁ i SC₂ Co nie ma wpływu na ostateczne rozwiązanie

Piotr 10: bezendu możesz mi podać wynik do tego zadania, bo chcę sprawdzić czy dobrze zrobiłem ?

Piotr 10: A przepraszam już został wynik podany. Cofam pytanie

ccc:

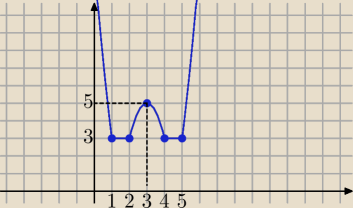
bezendu: Zbadaj przebieg zmienności funkcji f(x)=|x²−6x+8|+|x²−6x+5| Jest możliwość zrobienia tego zadania bez rysowania wykresu tej funkcji ?

ccc: https://matematykaszkolna.pl/forum/61910.html

bezendu: to są pochodne ?

ccc: Jeżeli bez pochodnych to musisz częściami narysować ten wykres! i podać własności : D_f, ZW_f , miejsca zerowe , punkty ekstremalne i monotoniczność

bezendu: nie miałem pochodnych, a sposobem licealnym to tylko wykres i właśnie stąd moje pytanie ale trudno trzeba rysować

ccc:

bezendu: to nie jest chyba dobry pomysł na to zadanie

ccc:

bezendu: z tego linku co mi podałaś to wiem jak wyznaczyć te przedziały ale dalej nie wiem jak działać na tych pochodnych

Mila: Ad. 19:22 To jest ładny wykres. Na jakiejś maturce próbnej była treść: Podaj liczbę rozwiązań równania : |x²−6x+8|+|x²−6x+5|=m w zależności od parametru m. warto rozwiązać to zadanie.

bezendu: Mila czyli jak w zależności od parametru m to rysuję ten wykres i prostą k i wtedy przesuwając patrze ile rozwiązań w danym przedziale

Mila: Rozwiązuj bez pochodnych. Podaj wzory funkcji dla przedziałów........

Mila: Tak, ad.19:58 wypisz wzory funkcji, to sprawdzę.

ccc:

ccc: Dobra, to ja spadam

bezendu: czyli teraz jak mam ten wykres od Ety to: (−∞,3) 0 rozwiązań <3,5) 4 rozwiązania {5} 3 rozwiązania (5,∞) 2 rozwiązania

ccc: dla m=3 nieskończenie wiele rozwiązań ( bo f(x) jest stała) dla m∊(3,5) −−4 rozwiązania reszta ok

bezendu: ok to idę robić kolejne zadanka dziękuje

ccc: Za gorąco

bezendu: w weekend było cieplej i zadanek nie robiłem

ccc: U mnie 36^o a w domu 30^o !

bezendu: ale ja nie byłem w domu korzystałem w wakacji

bezendu: Eta mieszkasz w województwie wielkopolskim ?

ccc: ...w mazowieckim

bezendu: etam

ccc: etam

bezendu:

ccc: