Rozwiąż nierówność aaa: 1. Rozwiąż nierówność: 3(x−1)*√−(x−1)(x+9)≥0 2. Zbadaj przebieg zmienności funkcji f(x)=|x²−6x+8| + |x²−6x+5| f(X)=|(x−2)(x−4)| + |(x−1)(x−5)|

aaa: ...?

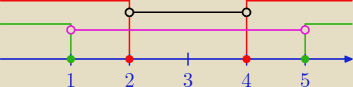
Godzio: x ∊ <−9,1> 3(x−1)*√−(x−1)(x+9) ≥ 0 −− wyrażenie pod pierwiastkiem jest zawsze ≥ 0 wiec wystarczy ustalić kiedy 3(x − 1) jest ≥ 0 x − 1 ≥ 0 ⇒ x ≥ 1, łącząc to z dziedziną otrzymujemy rozwiązanie: x ∊ {−9,1}

Godzio: Z tym przebiegiem mogę trochę pomóc, tylko napisz mi co na niego się składa a ja już zaczynam wyliczać

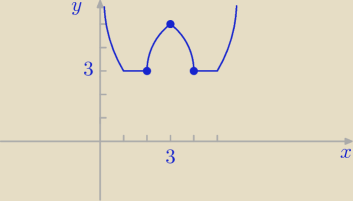
Godzio: Nic nie piszesz to w takim razie daje to co zrobiłem f(x) = |x² − 6x + 8| + |x² − 6x + 5| D = R ZW = <3,∞) Miejsca zerowe: brak x² − 6x + 8 ≥ 0 ⇒ |x² − 6x + 8| = x² − 6x + 8 ⇒ x ∊(−∞,2>∪<4,∞) x² − 6x + 8 < 0 ⇒ |x² − 6x + 8| = −x² + 6x − 8 ⇒ x ∊(2,4) x² − 6x + 5 ≥ 0 ⇒ |x² − 6x + 5| = x² − 6x + 5 ⇒ x ∊(−∞,1>∪<5,∞) x² − 6x + 5 < 0 ⇒ |x² − 6x + 5| = −x² + 6x − 5 ⇒ x ∊(1,5) 1^o x ∊(−∞,1>∪<5,∞) f(x) = x² − 6x + 8 + x² − 6x + 5 = 2x² − 12x + 13 2^o x ∊ (1,2>∪<4,5) f(x) = x² − 6x + 8 − x² + 6x − 5 = 3 3^o x ∊ (2,4) f(x) = −x² + 6x − 8 − x² + 6x − 5 = −2x² + 12x − 13 1^o x ∊(−∞,1>∪<5,∞) f(x) = 2x² − 12x + 13 f '(x) = 4x − 12 f '(x) > 0 ⇒ 4x > 12 ⇒ x > 3 −−− funkcja jest rosnąca dla x∊ <5,∞) i malejąca dla x ∊(−∞,1> f ''(x) = 4 −− funkcja na całym przedziale jest wypukła x ∊ (−∞,1>∪<5,∞) 2^o x ∊ (1,2>∪<4,5) f(x) = 3 −− funkcja stała 3^o x ∊ (2,4) f(x) = −2x² + 12x − 13 f '(x) = −4x + 12 f '(x) > 0 ⇒ 4x < 12 ⇒ x < 3 −− funkcja jest rosnąca dla x ∊ (2,3), malejąca x ∊ (3,4) f(3) = −2 * 9 + 12 * 3 − 13 = 5 ⇒ maksimum lokalne: P(3,5) f ''(x) = −4 −−− funkcja w całym przedziale jest wklęsła ⇒ x ∊ (2,4) Brak punktów przegięcia,

Godzio:

Basia: Godziu błąd w pierwszym x∊<−9,1> i x≥ 1 ⇔ x=1 ⇔ x∊{1}

Godzio: Nie, nie −9 też jest rozwiązaniem chodziło że żeby całe było równe zero to albo x = 1 albo x = −9 a żeby było większe od zera to x − 1 ≥ 0 bo pierwiastek jest zawsze większy równy zero

aaa: Mam pytanie do zadania 2. z wykresem dlaczego w przypadku gdzie jest f'(x) rozpatrujemy to jako funkcję liniową (f '(x) = 4x − 12) skąd ona się wzięła?

Pato: mam pytanie, dlaczego ta funkcja nie ma miejsc zerowych?

PW: Na to pytanie odpowiedzieć łatwo: bo jest sumą dwóch modułów − musiałyby być zerami oba jednocześnie, a to jest niemożliwe.

Pato: dziękuję ci bardzo ;>