Geometria zadania dla chętnych. Arczi: Zadanka dla maturzystów i chętnych poziom rozszerzony. Geometria zad1. Podstawa trójkąta równobocznego jest średnicą koła o promieniu r. Oblicz stosunek powierzchni części trójkąta leżącej na zewnątrz koła do pola powierzchni części koła leżącej wewnątrz koła. zad2. Bok trójkąta równobocznego T ma długość a. Ze środka ciężkości tego trójkąta zakreślono okrąg o

	1
promieniu długości		a, wyznaczający koło K. Oblicz pola figur T−K oraz K−T
	3

zad3. Na okręgu o promieniu 3 cm opisano trapez którego kąty przy dłuższej podstawie maja 30 i 60 stopni.Oblicz pole trapezu. zad4*. Na okręgu opisano trapez prostokątny. Odległość środka okręgu od końców dłuższej podstawy wynoszą 8√2 cm i 17 cm. Oblicz pole trapezu. zad5*. Rozważmy trapezy równoramienne, których obwód jest równy 2p, a kąt ostry ma miarę α. Wyznacz długość ramienia tego trapezu, który ma największe pole. zad6*. Romb o boku długości 18cm podzielono na trzy częśći o równych polach prostymi przechodzącymi przez wierzchołek kąta ostrego. Oblicz długości odcinków, na jakie te proste podzieliły boki rombu zad6. Bok kwadratu ABCD ma długość a. Na przeciwległych bokach AB i CD zbudowano trójkąty równoboczne, leżące wewnątrz kwadratu. Oblicz pole częśći wspólnej tych trójkątów. Dalej dodam zadania z innych działów, kto chcę niech rozwiązuje dla sportu.

Arczi: Ciąg arytmetyczny i geometryczny. zad7

	1		1		1
Liczy a,b,c tworzą ciąg arytmetyczny , natomiast liczby		,		,		tworzą
	a		b		a+b+c

ciąg geometryczny. Wyznacz iloraz ciągu geometrycznego. zad8 Trzy liczby które tworzą ciąg arytmetyczny dają w sumie 39. Jeśli od pierwszej i od trzeciej liczby odjąć 3 ,a od drugiej 5, to otrzymane różnice utworzą ciąg geometryczny. Znajdź liczby tworzące ciąg arytmetyczny zad9. Trzy liczby które tworzą ciąg geometryczny dają w sumie 35. Jeśli od pierwszej i od trzeciej liczby dodać 4 ,a do drugiej 5, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź liczby tworzące ciąg geometryczny Te zadania na czerwono są ponad maturę. zad10. Udowodnij, że w nieskończonym ciągu geometrycznym zbieżnym, w którym a₁q≠0, stosunek każdego wyrazu sumy wszystkich następnych wyrazów jest stały. Jaki powinien być iloraz takiego ciągu, aby każdy wyraz równał się pięciokrotnej sumie wszystkich następnych wyrazów. zad11. Rozwiąż nierówność

	1		1
U{1]{x+1}+		+		+...≤3x−2
	(x+1)2		(x+1)3

zad12. Balon wzniósł się w ciągu godziny na wysokość 4000m.Jaka jest graniczna wysokość, którą mógłby

	1
osiągnąc balon, gdyby w ciągu każdej następnej godzinty wznosił się na wysokość równą
	3

wysokości z godziny poprzedniej? zad13.

	9
Suma wyrazów nieskończonego ciągu geometrycznego zbieżnego wynosi		, a drugi wyraz ciągu
	2

równa się 1. Wyznacz ten ciąg.

Janek191: Np. z.8 a,b,c − ciąg arytmetyczny, więc b − a = c − b ⇒ 2 b = a + c a + b + c = 39 ⇒ ( a + c) + b = 39 ⇒ 2b + b = 39 ⇒ 3b = 39 b = 13 −−−−− a − 3, b − 5, c − 3 − ciąg geometryczny, więc ( b −5)² = ( a − 3)*( c − 3) a + c + 13 = 39 ⇒ c = 26 − a zatem ( 13 − 5)² = ( a − 3)*(26 − a − 3) 64 = (a − 3)*( 23 − a) 64 = 23 a − a² − 69 + 3a a² − 26 a + 133 = 0 Δ = ( −26)² − 4*1*133 = 676 − 532 = 144 √Δ = 12

	26 − 12		26 + 12
a =		= 7 ∨ a =		= 19
	2		2

więc c = 26 − 7 = 19 ∨ c = 26 − 19 = 7 Odp. a = 7 , b = 13, c = 19 lub a = 19, b = 13, c = 7 ===================================================

Janek191: Np. z.8 a,b,c − ciąg arytmetyczny, więc b − a = c − b ⇒ 2 b = a + c a + b + c = 39 ⇒ ( a + c) + b = 39 ⇒ 2b + b = 39 ⇒ 3b = 39 b = 13 −−−−− a − 3, b − 5, c − 3 − ciąg geometryczny, więc ( b −5)² = ( a − 3)*( c − 3) a + c + 13 = 39 ⇒ c = 26 − a zatem ( 13 − 5)² = ( a − 3)*(26 − a − 3) 64 = (a − 3)*( 23 − a) 64 = 23 a − a² − 69 + 3a a² − 26 a + 133 = 0 Δ = ( −26)² − 4*1*133 = 676 − 532 = 144 √Δ = 12

	26 − 12		26 + 12
a =		= 7 ∨ a =		= 19
	2		2

więc c = 26 − 7 = 19 ∨ c = 26 − 19 = 7 Odp. a = 7 , b = 13, c = 19 lub a = 19, b = 13, c = 7 ===================================================

Janek191: z.13

	a1
S =
	1 − q

zatem

a1		9
	=		⇒ 2 a1 = 9*( 1 − q) = 9 − 9q
1 − q		2

	1
a2 = a1 *q = 1 ⇒ a1 =
	q

więc

	1
2*		= 9 − 9q / * q
	q

2 = 9q − 9q² 9q² − 9q + 2 = 0 Δ = ( −9)² − 4*9*2 = 81 − 72 = 9 √Δ = 3

	9 − 3		1		9 + 3		2
q =		=		∨ q =		=
	18		3		18		3

zatem

	1		1		3
a1 =		= 3 ∨ a1 =		=
	13		23		2

Odp. Dwa ciągi spełniają warunki zadania:

	1
1) a1 = 3 i q =
	3

	3		2
2) a1 =		i q =
	2		3

=============================

5-latek: Wskazowka do zadania nr 2.

	1
Punkty przeciecia okregu z bokami trojkata tworza szesciokat foremny o boku		a
	3

Janek191: z.11

1		1		1
	+		+		+ ... ≤ 3x − 2
x+1		(x+1)2		(x + 1)3

Lewa strona , to suma nieskończonego ciągu geometrycznego dla

	1		1		1
a1 =		i q =		, x ≠ − 1 I		I < 1
	x+ 1		x+1		x + 1

	a1
S =
	1 − q

więc

	1		1		1		1 + x		1
S =		: [ 1 −		] =		: [		−		] =
	x + 1		1 + x		x+1		1+ x		x + 1

	1		x		1		x + 1		1
=		:		=		*		=
	x + 1		x + 1		x + 1		x		x

Mamy więc nierówność

1
	≤ 3 x − 2
x

1) x ≥ 0 ∧ 1 ≤ 3 x² − 2 x 2) x < 0 ∧ 1 ≥ 3 x² − 2 x 3 x² − 2 x − 1 ≥ 0 ∧ x ≥ 0 Δ = 4 − 4*3*(−1) = 16 √Δ = 4

	2 − 4		−1		2 + 4
x =		=		∨ x =		= 1
	6		3		6

zatem x ∊ < 1; +∞ ) −−−−−−−−−−−−−−−−−−− 3 x² − 2 x − 1 ≤ 0 ∧ x < 0

	− 1
x =		∨ x = 1
	3

	−1
zatem x ∊ (		; 0 )
	3

−−−−−−−−−−−−−−−−−−−−−−−− Ma być

	1
I		I < 1
	x + 1

	1
Dla x ∊ < 1; + ∞ ) jest I		I < 1
	x + 1

	−1		1
Dla x ∊ (		; 0 ) jest I		I > 0 − odpada
	3		x + 1

Odp. x ∊ < 1 ; + ∞ ) ==================

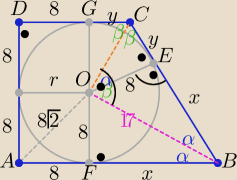
Eta: zad.4 r=8 z tw. Pitagorasa w trójkącie FBO x= √17²−8² = 15 bo x>0 Z podobieństwa trójkątów BOE i COE z cechy (kkk)

	y		r		r2		64
		=		⇒ y=		=
	r		x		x		15

P(tr)= 2P(kwadratów) + 2P(ΔFBO)+2P(ΔCEO) bo małe trójkąty są parami przystające

	1		1
P(tr)= 2*64 +2*		*x*8+2*		*y*8
	2		2

	512		2
P(tr)= 128+ 120+		= 282		[j2]
	15		15

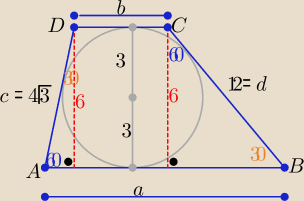
Eta: r=3 , 2r=h= 6 Z własności trójkątów o kątach 30^o, 60^o, 90^o ( lub z funkcji trygonometrycznych) c=4√3 i d= 12 Z warunku opisania czworokąta na okręgu: a+b= c+d ⇒ a+b= 4√3+12

	a+b
P(tr)=		*2r= (a+b)*r
	2

P(tr)= ...... = 12(√3+3) [j²]

pigor: ..., zad. 5*. Rozważmy trapezy równoramienne, których obwód jest równy 2p, a kąt ostry ma miarę α. Wyznacz długość ramienia tego trapezu, który ma największe pole. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− niech x=? − szukana długość ramienia trapezu o podstawach b<a i wysokości h, to z warunków zadania : 2x+a+b= 2p ⇔ a+b= 2(p−x) i 0< x< p, zatem jego pole w funkcji od x : P(x)= ¹₂(a+b)h= (p−x)xsinα= −sinα x(x−p) = P_max ⇔ x= ¹₂(0+p) ⇔ ⇔ x= ¹₂p −, czyli gdy ramię trapezu jest czwartą częścią jego obwodu. ...

Arczi: jeszcze takie praktyczne zadanie dla maturzystów ,gdyż sporo z nich w szkole średniej łapie zły nawyk jarania fajek Ktoś zaczął palić papierosy po skończeniu 16 lat i od tej pory na papierosy wydawał średnio 200 zł miesięcznie. Jeśli roczny wydatek na papierosy wpłaciłby do banku w końcu każdego roku, to jaką sumę zaoszczędziłby z końcem 60 roku życia? Zakładamy że oprocentowanie w banku wynosi 6%, kapitalizacja odsetek następuje raz na rok.

Saizou: sformulowanie 'wplacil do banku' tyczy sie czego? xd bo np. mozna wplacic na konto, lub lokate.

Piotr: q=1,06(6%+wartość podstawowa) n=60−16=44 a₁=200*12=2400 [zł]

	1−q42		−11,985471
S44=a1		=2400		=479418,84 [zł]
	1−q		−0,06

Saizou : Piotr a co jeśli lokata była nieodnawialna

Janek191: z.12

	1
Mamy nieskończony ciąg geometryczny o a1 = 4 000 i q =
	3

więc jego suma

	a1		4 000		4 000		3
S =		=		=		= 4 000*		= 6 000
	1 − q		1 − 13		23		2

Odp. Graniczna wysokość balonu, to 6 000 m. ====================================

Piotr: Saizou nie kombinuj

Saizou : nic nie kombinuję tylko 'logicznie myślę'

Piotr: Aż mnie to zaciekawiło i Właśnie zrobiłem podobne zadanko, ze zbioru K. Pazdro i zrobiłem w ten sam sposób rozumowania i wyszedł wynik taki jak w odpowiedzi

Saizou : yy........cofam to co napisałem bo on przecież wpłaca co roku 2400zł więc chcąc nie chcąc jest ciągłość w wzroście pieniędzy

Piotr: masz Saizou bo się nudzisz ''Wyznacz taki punkt A na prostej 2x + y − 1 = 0 , by suma kwadratów jego odległości od osi układu była najmniejsza''.

Saizou : niech punkt A(x;−2x+1) odległość od osi x to l−2x+1l odległość od osi y to lxl l−2x+1l²+lxl² ma być najmniejsza (−2x+1)²+x²= 1−4x+4x²+x²=

	4		2
5x2−4x+1 najmniejsza wartość jest dla xw=		=
	10		5

	2		4		1
−2*		+1=−		+1=
	5		5		5

	2		1
A(		:		)
	5		5

czy jakoś tak

Piotr: Dobrze

Saizou : 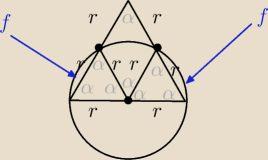zadanie 1 α=60

	1		√3		1
Ptrójkąta poza kołem=Pr−Pw=r2*sin60−		*πr2= r2(		−		π)
	6		2		6

P_{koła poza trójkątem}=2*P_f+P_{1/2 koła}

	1		r2√3		1		1		√3
Pf=Pw−PΔ=		πr2−		=		r2(		π−		)
	6		4		2		3		2

	1		1		√3		1
Pkoła poza trójkątem=2*		r2(		π−		)+		πr2=
	2		3		2		2

	1		√3		1		5		√3
=r2(		π−		+		π)=r2(		π−		)
	3		2		2		6		2

	√3   1   r2( − π)   2   6		3√3−π
stosunek		=
	5   √3   r2( π− )   6   2		5π−3√3

jak się gdzieś nie kopnąłem

ccc:

	3√3−π
Odp: ....=
	3√3+π

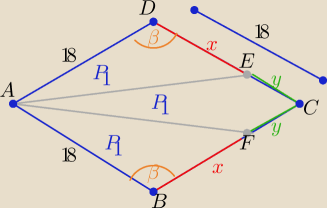
ccc: zad.4)

	1
P1=P(AED)=		*18*x*sinβ= 9xsinβ
	2

	1
z treści zadania P1=		P(rombu)
	3

P(rombu)= 18*18*sinβ

	1
9xsinβ=		*18*18*sinβ ⇒ 9x=6*18 ⇒x= 6
	3

x=|DE|=|BF|= 12 cm , y=|FC|=EC|= 6 cm

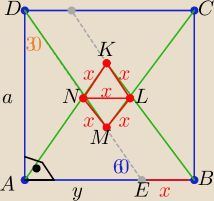
ccc: zad 6) ( jeden ze sposobów) Część wspólna jest rombem KLMN o boku "x" i kącie ostrym 60^o

	x2√3
P(KLMN)= x2*sin60o=
	2

	a		a		a√3
z trójkąta AED		= tg60o to y=		=
	y		√3		3

	a√3		a
x= a−y = a−		=		(1−√3)
	3		3

	a2
P(KLMN)= .......... =		(2√3−3) [j2]
	3

Saizou : skąd ja znam take sposoby przedstawiania zadań, które są rozwiązywane przez ccc

ccc: A no nie wiem?

Saizou : hehe jasnowidz ze mnie xd

ccc:

Saizou : a wcześniej byłaś krecikiem później jakoś mkf czy coś takiego teraz ccc

ccc: Ojj .... było tego, było

Saizou : hehe trzeb by coś policzyć wreszcie w te wakacje, ale jakoś nic się nie chce, za gorąco

ccc: @Saizou fajny dowodzik Wykaż,że dla dodatnich liczb x,y,z zachodzi:

	1		1		1		3
		+		+		≥
	x(1+y)		y(1+z)		z(1+x)		1+xyz

Saizou : stawiam na nierówność między średnimi

5-latek: https://matematykaszkolna.pl/forum/208586.html.....Saizou. Zobacz na oststni post tutaj bo nie w tym linku wstawilem

5-latek: https://matematykaszkolna.pl/forum/208586.html Jeszcze raz

ccc:

bezendu: Eta ładnie się tak podszywać pod maturzystów ?

ccc: bezendu .........

bezendu: zajączek,mmk,aTe,Klara,ccc=Eta