Trygonometria Kocham kobiety : Od czego zacząć uczyć się trygonometrii ? Za rok mam maturę i chciałbym to opanować bardzo dobrze ale niektóre równania sprawiają mi problem

Kocham kobiety : sin3x=1

	π
sin3x=sin
	2

	π
3x=		+2kπ /3
	2

	π		2
x=		+		kπ
	6		3

ok ?

fx: Naucz się teorii i wzorów. Następnie mając już jakiejś podstawy zabierz się za zadania − należy wykształcić sprawność rachunkową, którą inną drogą niż licząc zadania − nie zdobędziesz. Gdy pojawią się wątpliwości pytaj na forum ale pamiętaj − zawsze wpierw sam próbuj poradzić sobie z problemem, chociaż wymyślić założenia, coś zauważyć − nic tak nie uczy jak własne próby dojścia do rozwiązania. Na forum zaznaczaj, że prosisz o wskazówki − więcej na tym zyskasz niż na gotowcach. Równania wygląda ok.

bezendu: ale jeszcze piszę się k∊C https://matematykaszkolna.pl/strona/1579.html

krystek: https://matematykaszkolna.pl/strona/3421.html

krystek: Rozwiąz :

	1
sinx=
	2

	1
sinx=−
	2

Kocham kobiety :

	1
sinx=
	2

sinx=sinU{π}[6}

	π		5
x=		+2kπ lub x=		π+2kπ
	6		6

	1
sinx=−
	2

	π
sinx=−
	6

	π		7
x=−		π+2kπ lub x=		π+2kπ
	6		6

k∊C ok ?

krystek:

	π
zapis :sinx=−sin		i bedzie ok
	6

Przeszukaj na forum masz b dużo zadań

	1
sin2x=
	2

krystek: Zapisz zadania z którymi masz problem

Kocham kobiety : problem mam z trudniejszymi równaniami

krystek: masz mnóstwo ich na forum !

krystek: https://matematykaszkolna.pl/forum/201620.html

Kocham kobiety : @krystek na razie nie chcę robić z wartością bezwzględną po kolacji wstawię jakieś zadania których nie rozumiem

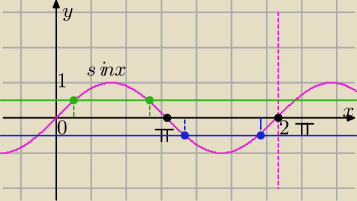
Mila: Ja rozwiązuję tak:

	1
sin(x)=
	2

	π		π
x=		+2kπ lub x=(π−		)+2kπ i k∊C
	6		6

	−1
sin(x)=
	2

	π		5
x=π+		+2kπ lub x=		π+π+2kπ⇔
	6		6

	7π		11π
x=		+2kπ lub x=		+2kπ
	6		6

II sposób

	−1
sin(x)=
	2

	π		7π		π		11π
x=π+		+2kπ=		+2kπ lub x=2π−		+2kπ=		+2kπ
	6		6		6		6

Kocham kobiety : @Mila czyli moje rozwiązanie jest nie poprawne

Kocham kobiety :

	1
sin2x=
	2

	√2		√2
sinx=		lub sinx=−
	2		2

i tu będą 4 rozwiązania ?

	√2		√2
dwa dal sinx=		i dwa dla sinx=−
	2		2

Mila: Sprawdzam Twoje rozwiązanie: jedno zgadza się z moim, drugie:

	−π
x=		+2kπ
	6

	−π		11
jeśli k=1 to masz x=		+2π=		π
	6		6

Jest też poprawne, każdy wybiera sam swoją ścieżkę do wiedzy. Masz rysunek i popatrz jak układają się te rozwiązania. Chodzi o to , że "spotkasz" różne odpowiedzi i musisz umieć sprawdzić , czy Twoje rozwiązanie jest prawidłowe.

Kocham kobiety : ja robię tak właśnie

	π		π		7
jeśli jedno mam −		to drugie π−(−		)=		π+2kπ ?
	6		6		6

Mila: Wpisz rozwiązania z godz. 21:43.

pigor: .... , lub do wyboru i koloru (bez wykresu) np tak : sinx= −¹₂ ⇔ −sin(π+x)= −¹₂ ⇔ sin(π+x)= ¹₂ ⇔ ⇔ π+x= ¹₆π+2kπ lub π+x= π−¹₆π+2kπ ⇔ ⇔ x= −⁵₆π+2kπ lub x= −¹₆π+2kπ i tu można zakończyć, ale dobrze jest podawać w odpowiedzi kąty ostre dodatnie, więc "zabieram" okres 2π z z wielokrotności k*2π=2kπ) ⇔ ⇔ x= −⁵₆π+2π+2kπ lub x= −¹₆π+2π+2kπ ⇔ ⇔ x= ⁷₆π+2kπ lub x= ¹¹₆π+2kπ i koniec, a "idąc" dalej ⇔ x= ¹₆π(7+12k) lub x= ¹₆π(11+12k) , gdzie k∊C i taką odpowiedź lubię najbardziej . ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− analogicznie możesz potraktować ... sinx= −¹₂√2

Kocham kobiety :

	√2
sinx=
	2

	π
sinx=sin
	4

	π		π
x=		+2kπ lub x=π−		+2kπ k∊C
	4		4

	√2
sinx=−
	2

	π
sinx=−sin
	4

	π		π
x=−		+2kπ lub x=π+		+2kπ
	4		4

pigor: ... możesz "pojechac" dalej x= −¹₄π+2kπ = −¹₄π+2π+2kπ= = ⁷₄π+2kπ = ¹₄π(7+8π) i k=0,±1,±2, ... . ...

Kocham kobiety : @pigor a wyniki są ok ?

Kocham kobiety : jeszcze post 21:58 dopiero zaczynam swoją przygodę z trygonometrią dlatego będę pytał aż do skutku

pigor: .... tak o.k., tylko, że często (w porządnych zbiorach zadań itp) może nie być odpowiedzi z kątem ujemnym i będziesz w kropce dlatego ci pokazuję co masz zrobić. ...

Kocham kobiety : ale na maturze chyba uznają takie coś ? oczywiście wszystkie wskazówki zapisuje w zeszycie a Ty jesteś dobrym matematykiem więc wskazówki tez dobre

pigor: ..., myślę, że zadasz te swoje pytania po wakacjach na lekcjach matmy i otrzymasz odpowiedzi cię satysfakcjonujące . , bo np. ja musiałem podawać odpowiedzi dodatnie (w przedziale (0;2π) lub (0;π) i było fajnie

Mila: Na maturze też często proszą o rozwiązania z przedziału <0,2π>.

pigor: ...no widzisz, to już masz jasną sprawę. ...

Kocham kobiety : @Mila ale jak mam przedział <0,2π> to wypisuje tylko rozwiązania dodatnie ?

Kocham kobiety : ?

Mila: Tak, możesz rozwiązać Twoim sposobem i "przesunąć" o 2π, w przypadku sinx i cos x.