matura - z czego się uczyć?
sdt: za 300 dni matura, ja w tym roku szkolnym uczyłem się 5 razy po 2h zadań do sprawdzianów i to
bardziej na pamięć niż na zrozumienie...
z czego mi polecacie zacząć się uczyć (chciałbym na wakacjach trochę przerobić)?
celuję w podstawę +90% i rozszerzenie ponad 60−70. wiem, że to możliwe, bo kolega się w miesiac
przygotował, a wcale orłem z matmy nie był.
15 lip 21:25
bezendu:
zbiór Andrzeja Kiełbasy podstawa+rozszerzenie
aksjomat czerwony poziom roz
oficyna edukacyjna poziom rozszerzony
do podstawy przerabiam operon
i do tego zadnia info i arkusze z ubiegłych lat

15 lip 21:28
Garth: Moze przedstaw wpierw, jaki jest Twoj poziom, z czym masz problemy.
Jednym z najbardziej popularnych i polecanych zbiorow zadan sa zbiory Andrzeja Kielbasy.
15 lip 21:28
Piotr: Polecam Krzysztof Pazdro− Oficyna Edukacyjna. Jest tam poziom zarówno podstawowy jak i
rozszerzony

.
15 lip 21:32
sdt: poziom raczej słaby, ale tak często jest. kolega pisał próbne w styczniu z rozsz. na 14−20% a w
maju napisał na 88 bodajże
myślę, że podstawę tak na 60% (słabo, wiem) a z rozszerzenia to tak średnio gdzieś 2 zadania
zrobię
15 lip 21:37
bezendu: proponuje przerobić najpierw zadania z podstawy a potem brać się za rozszerzenie

nie ma
sensu robić rozszerzenia mając braki w podstawie

Powodzenia w nauce

15 lip 21:38
sdt: dz, ale nie chciałbym się uczyć schematycznie, ale wiem, że da się tak zdać, bo matury są do
siebie bardzo podobne (mowa o podstawie)
także reasumując, to oe i kiełbasa tak?
15 lip 21:41
bezendu:
jakie schematycznie

wybij to sobie z głowy, matematyki nie uczymy się na pamieć to nie
historia..
15 lip 21:43
Piotr: Kiełbasa może być za ciężki dla Ciebie od razu. Są tam naprawdę trudne zadania takich ,których
na maturze nie będzie.
15 lip 21:43
Piotr: Tak jest
bezendu 

15 lip 21:45
bezendu: kiełbasa jest dobra właśnie na początek

uczy myślenia i pozwoli nadrobić braki

15 lip 21:45
Eta:

15 lip 21:46
Piotr: Szczególnie jak się trafi na dział ''Planimetria''

15 lip 21:46
bezendu: Cześć
Eta 
15 lip 21:47
Eta:
Cześć, cześć


.... obydwa nie są robaczywe

15 lip 21:48
bezendu: wole <czereśnie> i to prosto ze sadu

15 lip 21:49
Eta:
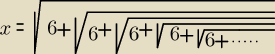
zad1/ wykaż,że liczba : x jest całkowitą
15 lip 21:57
Eta:
zad2/ Liczby dodatnie a,b,c są długościami boków trójkąta
Wykaż,że: a(b−c)2+b(c−a)2+c(a−b)2+4abc> a3+b3+c3
15 lip 22:00
Eta:
zad3/Wykaż,że liczba sin10o jest pierwiastkiem wielomianu
W(x)=8x3−6x+1
15 lip 22:02
Eta:
zad4/ Wykaż,że liczba : L=14+24+34+..... +20114
jest parzysta
15 lip 22:04
Eta:
zad5/ Wykaż,że jeżeli α i β są kątami trójkąta, takimi,że
to trójkąt jest prostokątny lub równoramienny
Powodzenia przyszli maturzyści

15 lip 22:09
bezendu:
8*(sin100)3−6(sin100)+1=0
8sin3100−6sin100+1=0
2(4sin3100−3sin100)+1=0
jak to dalej ruszyć ?
15 lip 22:12
Piotr: Moge ja do zadania pierwszego?
15 lip 22:13
bezendu: @Piotr rozwiązuj

15 lip 22:14
Eta:
@
bezendu ............. nie ma tak lekko

myśl ................. aż do skutku

15 lip 22:15
Eta:
Jasne

wszyscy maturzyści mogą podawać swoje rozwiązania
15 lip 22:16
Piotr: Zrobilem te 1 zadanie tylko problem mam z zapisaniem tego tutaj, mam na mysli tych pierwiastkow
15 lip 22:17
Eta: Podaj odp do zad 1/
15 lip 22:18
Piotr: Wyszlo mi ze x=3 , x=−2 odrzucilem gdyz x≥0
15 lip 22:19
Eta:
zad1/ Ok

15 lip 22:20
Piotr: 

15 lip 22:22
sdt: a co powiecie o uczenie się z filmików na internecie tak aby załapać dany dział?
15 lip 22:22
bezendu: zadanie 3

i nie wiem co dalej ?

za wskazówkę ?

15 lip 22:22
Eta:
Działaj z następnymi

15 lip 22:23
bezendu: ja polecam robić zadanie od
Ety wtedy już dużo do szczęścia na potrzeba

15 lip 22:23
Eta:
Hehe
bezendu ..... jak Ci podpowiem, to będzie koniec dowodu

Myśl dalej .............................................................
15 lip 22:25
Eta:
No dobra

przekupiłeś mnie

wyprowadź wzór na sin3α=........... ( nie z tablic, tylko wyprowadź !
15 lip 22:29
Eta:
A ja idę na
herbatkę 
15 lip 22:30
bezendu: właśnie o to chodzi

4sin
310
0−3sin
210
0
−sinα(3−4sin
210
0)
−sin3*10
0
15 lip 22:33
sdt: w jakiej kolejności polecacie przerabiać działy?
15 lip 22:35
bezendu: tak jak tutaj jest zamieszczone na stronie

15 lip 22:36
Eta:
A no........"właśnie o to chodziło"

15 lip 22:39
bezendu: dajmy na to zadanie za 5 punktów czyli już 10 % Eta mam pytanie do Ciebie ?
15 lip 22:40
Eta:
Pytaj

15 lip 22:42
15 lip 22:42
sdt: W tej OE (podręcznik) jest strasznie dużo do czytania. Opłaca się to czytać w ogóle?
Czy wy bierzecie jakąś teorię przed robieniem zadań z nowego działu, a jeśli tak to skąd?
15 lip 22:42
bezendu: teorie masz w książkach należy się nauczyć i potem stosować w praktyce jeszcze jakieś pytania
?
15 lip 22:44
sdt: czy teoria z tej strony wystarczy, aby "wkręcić się" w robienie zadań?
15 lip 22:46
Eta:
@
bezendu
Z programu nauczania, niestety,ale "wyrzucono" (a szkoda) dział z sumą ciągu zbieżnego
Kiedyś,takie zadania były baaaardzo często na maturze
a swoją drogą wcale nie należą do trudnych

15 lip 22:47
bezendu:
14+24+34+..... +20114
14+14*24+14*34+.....14*20004
14(1+24+34+.......20004)
1(1+16+81+....)
w nawiasie otrzymamy liczbę parzystą więc mnożąc razy 1 ta liczb będzie parzysta ?
15 lip 22:52
bezendu:
właśnie nie jest trudne

15 lip 22:52
bezendu:
14+14*24+14*34+....14*20114
14(1+24+34+...20114)
1(1+16+81+...20114)
15 lip 23:01
Eta:
Hehe ......... 0 dowodu !
15 lip 23:06
bezendu: jak to zero dowodu


dziś i tak już nic nie wymyśle

dobranoc muszę się z tym przespać
15 lip 23:07
Eta:

15 lip 23:07
bezendu: 

15 lip 23:09
Eta:
No to jeszcze dodatkowo .......wykaż ,że ta liczba jest podzielna przez
503 
15 lip 23:11
Piotr: Zadanie 2
a(b−c)2+b(c−a)2+c(a−b)2+4abc>a3+b3+c3
a(b2−2bc+c2)+b(c−a)2+c(a2−2ab+b2)+4abc>a3+b3+c3
ab2−2abc+ac2+b(c−a)2+ca2−2abc+cb2+4abc>a3+b3+c3
ab3+ac3+b(c−a)2+ca3+cb3−a3−b3−c3>0
a2(c−a)+c2(a−c)+b2(a+c−b)+b(c−a)2>0
b2(a+c−b)>0, bo a+c>b oraz a>0,b>0,c>0
b(c−a)2>0
Ale jak a2(c−a)+c2(a−c) z tym sie uporać czy w zlą strone ide?
16 lip 10:10
Janek191:
z.4
14 + 24 + 34 + ... + 20114 =
= (14 + 34 + ... + 20114) + ( 24 + 44 + ... + 20104) =
suma 1006 liczb nieparzystych + suma 1005 liczb parzystych
Parzysta suma liczb nieparzystych jest liczbą parzystą.
Suma dowolnej ilości liczb parzystych jest liczbą parzystą.
Dana liczba jako suma dwóch liczb parzystych jest też liczbą parzystą.
16 lip 10:12
matematyka:
a
2(c−a)−c
2(c−a)
(c−a)(a
2−c
2)
(c−a)(a−c)(a+c)
−(a−c)
2(a+c)

16 lip 10:13
Piotr: Ale co z tego wynika? Bo tez tak probowalem robic
16 lip 10:14
matematyka: @Janek od kiedy TY jesteś maturzystą

problem z czytaniem post 22:16

16 lip 10:21
Piotr: @matematyka masz jakas wskazowke dla mnie do tego zadania z dowodem?
16 lip 10:22
matematyka: nie mogę Ci podać wskazówki

myśl aż do skutku jak mówi Eta

16 lip 10:25
Piotr: Ale to co napisales to nic z tego nie wynika chyba post z godz 10:13 bo a+c>0 , (a−c)2>0 ale
ten minus jest i on zmienia wszystko
16 lip 10:27
Janek191:
z.3
Korzystamy z wzoru
| | 1 | |
sin3 α = |
| ( 3 sin α − sin 3α) |
| | 4 | |
więc
| | 1 | |
W( sin 10O) = 8*[ |
| (3 sin 10o − sin 3*10o)] − 6 sin 10o + 1 = |
| | 4 | |
= 6 sin10
o − 2*sin30
o − 6 sin 10
o + 1 = − 1 + 1 = 0
16 lip 10:31
aniabb: [P[Piotr] wynika z tego że źle rozbiłeś..wyrzuciłeś dodatnie i została Ci jedna ujemna..sprawdź
co jest większe to co wyrzuciłeś czy to co Ci zostało

16 lip 10:35
Piotr: Później jeszcze pokombinuje

16 lip 10:36
ZKS:
Zrobiłem w inny sposób niż Piotr żeby mógł swoim sposobem dokończyć.
a(b − c)2 + b(c − a)2 + c(a − b)2 + 4abc > a3 + b3 + c3
Skoro to są boki trójkąta to
a + b > c ⇒ a + b − c > 0
b − a < c ⇒ a − b + c > 0
a − b < c ⇒ b − a + c > 0
(a + b − c)(a − b + c)(b − a + c) > 0
[a2 − (b − c)2](b − a + c) > 0
a2b − a3 + a2c − b(b − c)2 + a(b − c)2 − c(b − c)2 > 0
a2b − a3 + a2c − b3 + 2b2c − bc2 + ab2 − 2abc + ac2 − cb2 + 2bc2 − c3 > 0
a2b + a2c − bc2 + ab2 + ac2 − cb2 + 2b2c + 2bc − 2abc > a3 + b3 + c3
ab2 − 2abc + ac2 + bc2 − 2abc + a2b + a2c − 2abc + b2c + 4abc > a3 + b3 + c3
a(b2 − bc + c2) + b(c2 − 2bc + b2) + c(a2 − 2ab + b2) + 4abc > a3 + b3 + c3
a(b − c)2 + b(c − b)2 + c(a − b)2 + 4abc > a3 + b3 + c3
16 lip 11:25
Janek191:
z.4
Jest taki wzór
| | n*( n + 1)*(2 n + 1)*(3 n2 + 3 n − 1) | |
14 + 24 + ... + n4 = |
| |
| | 30 | |
więc
| | 2011*2012*4023*(3*20112 + 3*2011 − 1) | |
14 + 24 + ... + 20114 = |
| = |
| | 30 | |
| | 4*2011*4023*(3*20112 + 3*2011 − 1) | |
= 503* |
| − liczba podzielna przez 503 |
| | 30 | |
bo
4 dzieli się przez 2, 4023 dzieli się przez 3 i liczba w nawiasie dzieli się przez 5.
16 lip 12:11
ZKS:
Każdy zna ten wzór.

16 lip 12:13
Janek191:
Można znaleźć

Chodziło mi o sprawdzenie, czy rzeczywiście ta suma jest podzielna przez 503.
Z wzoru widać także, że ta suma jest liczbą parzystą.
Może ktoś znajdzie elementarny sposób rozwiązania tego zadania .
16 lip 12:47
Eta:
Witam Wszystkich "maturzystów"

16 lip 13:47
Eta:
Ze wzoru a4+b4=(a+b)(a3−a2b+ab2−b3)
14+20114 = 2012*(......) =2012*k, k€C
24+20104 = 2012*t
:
:
10054+10074= 2012*s
1006
i mamy:
L= 2012*(k+t+...+s)= 2012*u +1006 = ............ . u€C
c.n.u
16 lip 13:55
Saizou : Eto czy wynikiem
√6+√6+√6+...=
1 
16 lip 14:05
Eta:

.... x=3

16 lip 14:05
Saizou : no to pech, trzeba kombinować

16 lip 14:06
Eta:
Nie wierzę,że ni masz poprawnego wyniku

to łatwe zadanko
Myśl dalej.......

16 lip 14:09
Saizou : a no to może dlatego że się wczoraj balowało

16 lip 14:14
Eta:


16 lip 14:15
Saizou : wakacje są

16 lip 14:16
Janek191:
To ja mam takie zadania:
z.1
Podaj trójki liczb naturalnych spełniających układ równań :
x*y = z
x ! * y ! = z2
z.2
Podaj 30 piątek liczb naturalnych spełniających równanie
x + y + z + t + u = √x*y*z*t*u
z.3
Podaj 6 trójek liczb naturalnych spełniających równanie
x + y + z = x*y*z = √x3 + y3 + z3
gdzie
N = { 1,2,3, ... }
16 lip 14:22
Saizou : chyba już wiem
niech n=√6+√6+√6+√6+... /2 , bo L i P>0
n2=6+√6+√6+√6+...
n2=6+n
n2−n−6=0
(n−3)(n+2)=0
n=3 n=−2 (sprzeczność, bo n>0)
16 lip 14:26
zxcv:
Zad1
(x;y)={(3;4); (4;3)}
16 lip 14:49
zxcv:
Zad 3
(x;y;z)={(1;2;3); (1;3;2); (2;1;3); (2;3;1); (3;1;2); (3;2;1)}
16 lip 15:03
Piotr: a(b−c)
2+b(c−a)
2+c(a−b)
2+4abc>a
3+b
3+c
3
a(b
2−2bc+c
2)+b(c−a)
2+c(a
2−2ab+b
2)+4abc>a
3+b
3+c
3
ab
2−2abc+ac
2+b(c−a)
2+ca
2−2abc+cb
2+4abc>a
3+b
3+c
3
b
2(a+c−b)+a(c
2−a
2)+c(a
2−c
2) > 0
b
2(a+c−b)+a(c−a)(c+a)+c(a−c)(a+c) >0
b
2(a+c−b)+(a+c)[a(c−a)+c(a−c)] > 0
b
2(a+c−b)+(a+c)(2ac−a
2−c
2) > 0
b
2(a+c−b)>0 , gdyż a+c>b ; a+c>0
(2ac−a
2−c
2) <== ?
Jak to dalej robić? proszę o pomoc

16 lip 15:18
ZKS:
2ac − a2 − c2 = −(a − c)2
16 lip 16:10
Janek191: @zxcv
z.1 − brak wszystkich rozwiązań
z.3 Zamiast = powinno być ∊
16 lip 16:25
ZKS:
pigor ale niestety nie zgodzę się z Tobą chodzi mi dokładnie o zwroty tych nierówności
a + c < b ∧ a + b < c ∧ b + c < a?
Warunki trójkąta są inne
a + c > b ∧ a + b > c ∧ b + c > a
ale może się mylę.
16 lip 20:24
pigor: ... o kurcze, masz rację , ale gafę popełniłem , wstyd

, przepraszam , wywalcie toto

16 lip 21:34
Eta:

16 lip 22:03
Piotr: @ZKS i co z tego wynik ? −(a−c)
2<0 ?bo też tak próbowalem robic nie rozumiem tego, pomożesz mi
lub ktos inny?

16 lip 22:08
Piotr: podbijam
16 lip 22:22
ZKS:
Zrób jeszcze raz od początku bo prawie na samym początku masz źle.
b2(a + c − b) + a(c2 − a2) + c(a2 − c2) > 0
Tutaj już jest źle więc dalej też.
16 lip 22:34
Piotr: OK, niedlugo to poprawie

dzięki

16 lip 22:36
ZKS:
Nie ma za co proszę bardzo.

16 lip 22:38
pigor: ..., dzięki Eta,
16 lip 23:18
Eta:
Na zdrowie
pigor 

16 lip 23:21
pigor: ... . Wykaż, że jeżeli α i β są kątami trójkąta takimi, że
| sinα | | sinβ | |
| = |
| , to trójkąt jest prostokątny lub równoramienny . |
| cosβ | | cosα | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
mogę to rozwiązać, czy jeszcze nie

. ..

16 lip 23:23
Eta:
Proszę bardzo

(bo jakoś nikt z maturzystów się do tego zadania "nie pali"

16 lip 23:27
ZKS:
Hihi.

| sin(x) | | sin(y) | |
| = |
| |
| cos(y) | | cos(x) | |
sin(x)cos(x) = sin(y)cos(y)
sin(2x) = sin(2y)
sin(2x) − sin(2y) = 0
2sin(x − y)cos(x + y) = 0 ⇒ sin(x − y) = 0 ⇒ x = y ∨ cos(x + y) = 0 ⇒ x = 90
o − y.
16 lip 23:33
16 lip 23:35
pigor: ,,, , dzięki
Eta, może to mi się ... uda , no to np. tak :
| sinα | | sinβ | |
| = |
| ⇒ sinα*cosα = sinβ*cosβ /*2 ⇔ 2sinαcosα = 2sinβcosβ ⇔ |
| cosβ | | cosα | |
⇔ sin2α = sin2β ⇔ 2α = 2β lub 2α= 180
o−2β ⇔
⇔
α = β − Δ równoramienny lub
α+β= 90o − Δ prostokątny . c.n.w. ...

16 lip 23:44
pigor: ... . Liczby dodatnie a,b,c są długościami boków trójkąta.
Wykaż, że a(b−c)
2+b(c−a)
2+c(a−b)
2+4abc > a
3+b
3+c
3 .
−−−−−−−−−−−−−−−−−−−−−−−−−−
no to jeszcze raz ja , po ...

swojemu , dla własnych potrzeb
tak :
a(b−c)2+b(c−a)2+c(a−b)2+4abc > a3+b3+c3 ⇔
⇔ a(b−c)
2+b(c−a)
2+c(a
2+2ab+b
2) > a
3+b
3+c
3 ⇔
⇔ a(b−c)
2−a
3 + b(c−a)
2−b
3 + c(a+b)
2−c
3 > 0 ⇔
⇔ a[(b−c)
2−a
2] + b[(c−a)
2−b
2] + c[(a+b)
2−c
2] > 0 ⇔
⇔ a(b−c−a)(b−c+a) + b(c−a−b)(c−a+b) + c(a+b−c)(a+b+c) > 0 ⇔
⇔ a(b−c−a)
(b−c+a) − b
(b−c+a)(c−a+b) + c
(b−c+a)(a+b+c) > 0 ⇔
⇔
(b−c+a (ab−ac−a
2 − bc+ab−b
2 + ac+bc+c
2) > 0 ⇔ (a+b−c) (2ab−a
2−b
2+c
2) > 0 ⇔
⇔ (a+b−c) [c
2−(a−b)
2] > 0 ⇔
(a+b−c) (c−a+b)(c+a−b) > 0 , stąd i z nierówności Δ
jest to prawda dla a,b,c − długości boków Δ , no to c.n.w. . ...

17 lip 11:39

 .
.
 nie ma
sensu robić rozszerzenia mając braki w podstawie
nie ma
sensu robić rozszerzenia mając braki w podstawie  Powodzenia w nauce
Powodzenia w nauce 
 wybij to sobie z głowy, matematyki nie uczymy się na pamieć to nie
historia..
wybij to sobie z głowy, matematyki nie uczymy się na pamieć to nie
historia..


 uczy myślenia i pozwoli nadrobić braki
uczy myślenia i pozwoli nadrobić braki 




 .... obydwa nie są robaczywe
.... obydwa nie są robaczywe 

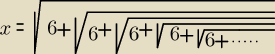 zad1/ wykaż,że liczba : x jest całkowitą
zad1/ wykaż,że liczba : x jest całkowitą


 myśl ................. aż do skutku
myśl ................. aż do skutku 
 wszyscy maturzyści mogą podawać swoje rozwiązania
wszyscy maturzyści mogą podawać swoje rozwiązania



 i nie wiem co dalej ?
i nie wiem co dalej ?  za wskazówkę ?
za wskazówkę ? 


 Myśl dalej .............................................................
Myśl dalej .............................................................
 przekupiłeś mnie
przekupiłeś mnie  wyprowadź wzór na sin3α=........... ( nie z tablic, tylko wyprowadź !
wyprowadź wzór na sin3α=........... ( nie z tablic, tylko wyprowadź !

 4sin3100−3sin2100
−sinα(3−4sin2100)
−sin3*100
4sin3100−3sin2100
−sinα(3−4sin2100)
−sin3*100






 dziś i tak już nic nie wymyśle
dziś i tak już nic nie wymyśle  dobranoc muszę się z tym przespać
dobranoc muszę się z tym przespać





 problem z czytaniem post 22:16
problem z czytaniem post 22:16 
 myśl aż do skutku jak mówi Eta
myśl aż do skutku jak mówi Eta 



 Chodziło mi o sprawdzenie, czy rzeczywiście ta suma jest podzielna przez 503.
Z wzoru widać także, że ta suma jest liczbą parzystą.
Może ktoś znajdzie elementarny sposób rozwiązania tego zadania .
Chodziło mi o sprawdzenie, czy rzeczywiście ta suma jest podzielna przez 503.
Z wzoru widać także, że ta suma jest liczbą parzystą.
Może ktoś znajdzie elementarny sposób rozwiązania tego zadania .


 .... x=3
.... x=3


 to łatwe zadanko
Myśl dalej.......
to łatwe zadanko
Myśl dalej....... 





 , przepraszam , wywalcie toto
, przepraszam , wywalcie toto 


 dzięki
dzięki 



 . ..
. .. 
 (bo jakoś nikt z maturzystów się do tego zadania "nie pali"
(bo jakoś nikt z maturzystów się do tego zadania "nie pali" 





 swojemu , dla własnych potrzeb
tak :
a(b−c)2+b(c−a)2+c(a−b)2+4abc > a3+b3+c3 ⇔
⇔ a(b−c)2+b(c−a)2+c(a2+2ab+b2) > a3+b3+c3 ⇔
⇔ a(b−c)2−a3 + b(c−a)2−b3 + c(a+b)2−c3 > 0 ⇔
⇔ a[(b−c)2−a2] + b[(c−a)2−b2] + c[(a+b)2−c2] > 0 ⇔
⇔ a(b−c−a)(b−c+a) + b(c−a−b)(c−a+b) + c(a+b−c)(a+b+c) > 0 ⇔
⇔ a(b−c−a)(b−c+a) − b(b−c+a)(c−a+b) + c(b−c+a)(a+b+c) > 0 ⇔
⇔ (b−c+a (ab−ac−a2 − bc+ab−b2 + ac+bc+c2) > 0 ⇔ (a+b−c) (2ab−a2−b2+c2) > 0 ⇔
⇔ (a+b−c) [c2−(a−b)2] > 0 ⇔ (a+b−c) (c−a+b)(c+a−b) > 0 , stąd i z nierówności Δ
jest to prawda dla a,b,c − długości boków Δ , no to c.n.w. . ...
swojemu , dla własnych potrzeb
tak :
a(b−c)2+b(c−a)2+c(a−b)2+4abc > a3+b3+c3 ⇔
⇔ a(b−c)2+b(c−a)2+c(a2+2ab+b2) > a3+b3+c3 ⇔
⇔ a(b−c)2−a3 + b(c−a)2−b3 + c(a+b)2−c3 > 0 ⇔
⇔ a[(b−c)2−a2] + b[(c−a)2−b2] + c[(a+b)2−c2] > 0 ⇔
⇔ a(b−c−a)(b−c+a) + b(c−a−b)(c−a+b) + c(a+b−c)(a+b+c) > 0 ⇔
⇔ a(b−c−a)(b−c+a) − b(b−c+a)(c−a+b) + c(b−c+a)(a+b+c) > 0 ⇔
⇔ (b−c+a (ab−ac−a2 − bc+ab−b2 + ac+bc+c2) > 0 ⇔ (a+b−c) (2ab−a2−b2+c2) > 0 ⇔
⇔ (a+b−c) [c2−(a−b)2] > 0 ⇔ (a+b−c) (c−a+b)(c+a−b) > 0 , stąd i z nierówności Δ
jest to prawda dla a,b,c − długości boków Δ , no to c.n.w. . ... 