l fx: https://matematykaszkolna.pl/forum/20377.html Będę wdzięczny za jakieś zadanko tego typu na poziomie rozszerzonej matury z matematyki . Dziękuję

Saizou : no to może coś takiego: 1) Miejsca zerowe dwóch funkcji liniowych są liczbami przeciwnymi. Wykresy tych funkcji przecinają się w punkcie (2;4)i wraz z OX ograniczają trójkąt o polu 12. Wyznacz wzory tych funkcji

fx: Odcinek |ω0X| = 4 i jest odległością punktu ω(2;4) od osi 0X. P(a, ω0X) = (ω0X * ) = 12 ⇔ a = 6 a = |ση| gdzie σ=(−x, 0), η(x, 0)

	⎧	x = 3
|−x| + |x| = 6 ⇔ 2|x| = 6 ⇔ |x| = 3 ⇔	⎨
	⎩	−x = 3

f(3) = 0 f(2) = 4 f(x) = 4x − 12 g(−3) = 0 g(2) = 4

	4x+12
g(x) =
	5

ok?

pigor: ... , f(x)= −4x+12 . ...

fx: U... 3a + b = 0 2a + b = 4 3a = −b a = −b/3

−2b
	+ b = 4
3

−b
	= 4
3

−b = 12 b = −12 f(3) = 3a − 12 = 0 3a = 12 a = 4 f(x) = 4x − 12 Gdzie mam błąd?

pigor: ..., znajdź sobie, bo nie chce mi się szukać, a widzę tylko, że punkt (2,4) nie spełnia twojego równania i tyle . ..

Saizou : wzory funkcji to f(x)=0,8x+2,4 h(x)=−4x+12

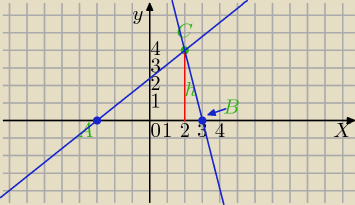
Mila: m: y=ax+b n: y=a'x+b' C=(2,4)

	1		1
PΔ=		|AB|*h⇔12=		*|AB|*4⇔|AB|=6
	2		2

C∊m, C∊n m: 4=2a+b i n: 4=2a'+b' m: y=ax+4−2a

	2a−4
ax+4−2a=0⇔ax=2a−4⇔x=
	a

	4−2a
−x=
	a

	2a−4		4−2a
|		−		|=6
	a		a

	2a−4−4+2a
|		|=6
	a

|4a−8|=6|a| 4a−8=6a lub 4a−8=−6a 2a=−8 lub −10a=−8

	8		4
a=−4 lub a=		=
	10		5

	2*(−4)−4
x=		=3
	−4

−x=−3 spr. m: y=−4x+12

	4		12
n: y=		x+
	5		5

fx: Mila , jak zawsze rozwiałaś wszystkie wątpliwości.

Mila: Zapomniałam, że nie trzeba rozwiązywać.

Saizou : można też tak

	4*a
12=
	2

a=6 zatem odległość od punktu (0:0) musi wynosić 3, bo miejsca zerowe są liczbami przeciwnymi,zatem przecinają oś X w punktach (3:0) oraz (−3:0) i wystarczy ułożyć równania prostych przechodzących przez 2 punkty