Funkcja kwadratowa nowy: O ile jednostek należy przesunąć parabolę y=−x²−4x−1 do góry, aby otrzymana parabola miała z parabolą y=x²−4x+5 dokładnie jeden punkt wspólny.

ICSP: o ile jednostek wiec załóżmy że o m przesuwamy parabolę do góry o m jednostek : y = −x² − 4x − 1 + m Szukamy punktów wspólnych(rozwiazujemy układ równań) y = −x² − 4x − 1 + m y = x² − 4x + 5 stąd : x² − 4x + 5 = −x² − 4x − 1 + m 2x² + 6 − m = 0 jeden punkt wspólny ⇒ jeden pierwiastek ⇒ Δ = 0 ⇒ m=6 Należy przesunąć o 6 jednostek w górę

nowy: ICSP, zajrzysz jeszcze tu? https://matematykaszkolna.pl/forum/208198.html

Mila: 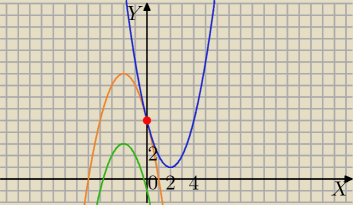y=−x²−4x−1 y=x²−4x+5 [a,b]=[0,b] wektor przesunięcia f(x)=−x²−4x−1 po przesunięciu o wektor [0,b] ma wzór : g(x)=f(x−0)+b g(x)=−x²−4x−1+b −x²−4x−1+b=x²−4x+5 ⇔ 2x²−b+6=0 2x²=b−6 ma jeden pierwiastek ⇔b−6=0 ⇔b=6 [0,6] wektor przesunięcia g(x)=−x²−4x+5 spr. −x²−4x+5=x²−4x+5 x=0 y=5

pigor: ... zauważmy, że tu |1|=|−1|=1 współczynników przy x² i różnica wyrazów wolnych 5−(−1)= 6 to składowa y szukanego wektora [0,6] przesunięcia . ...