Oblicz pole koła wpisanego w trójkąt Natalia: Najdłuższy bok trójkąta ABC ma 8 cm długości, a miary jego kątow są w stosunku 2:1:1. Oblicz pole trojkąta ABC oraz pole koła wpisanego w trojkąt ABC. Pole obliczyłam tak, proszę o sprawdzenie : 180st:2=90st 90st:2=45st. Dwa kąty są równe 45st, a jeden 90st więc jest to trójkąt prostokątny równoramienny. Najdłuższy bok ma 8 cm, czyli musi to być przeciwprostokątna, bo ona zawsze jest najdłuższa. Z Pitagorasa= x²+x²= 8² 2x²= 64 |:2 x²= 32 |√ x= 4√2 Mamy obliczone wszystkie boki: przeciwprostokątna=8 każda z dwóch przyprostokątnych=4√2 P=4√2*4√2/2=32:2= 16 tylko nie wiem jak obliczyć pole tego koła

Dziabong: Pole okręgu można by obliczyć z tego wzoru 542

Dziabong: Również można z wzoru z tablic maturalnych czyli a=4√2, b= 4√2, c = 8 r = p−c

	a+b+c
p=
	2

Albo z pola P = rp

Mila: 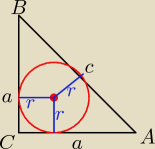Natalio, ustaliłaś, że to trójkąt prostokątny równoramienny.( patrz rysunek) c=8 ,= dł. przeciwprostokątnej

	1
PΔ=		a2
	2

c²=a²+a² 2a²=64 a²=32 a=4√2

	1
PΔ=		*32=16
	2

	a+a+c
PΔ=		*r
	2

	8√2+8
16=		*r
	2

16=((4√2+4)*r /*(4√2−4) [ wzór: (a−b)*(a+b)=a²−b²) 16*(4√2−4)=(32−16)*r r=4√2−4 P_◯=π*r² P_◯=π*(4√2−4)² dokończ