Napisz równanie natii: Napisz równanie prostej symetralnej przechodzącej przez punkt a i b. A=(3,4) B=(1,5)

camus: 1)https://matematykaszkolna.pl/strona/3385.html 2)znajdujesz to co ci potrzeba, tj. równanie prostej zawierającej AB i środek odcinka AB 3)znajdujesz symetralną

natii: Ale mi tu jakieś głupoty wychodzą...

5-latek: https://matematykaszkolna.pl/strona/1750.html i +to co camus i powinna byc gitara Napisz te glupoty na forum.

natii: nieee, heh

bez: a co gotowca chcemy?

natii: no co ty, to z powtórzenia, ale na klasówce pewnie będzie to samo ale zmienione dane. Ale nie wychodzi mi jak to gówno liczę..

natii:

PW: Samo pierwsze polecenie jest głupotą. Co to znaczy "prosta symetralna przechodząca przez punkt a i b?

natii: ja tego zadania nie konstruowałam, tak miałam napisane i próbuję to zrobić...

natii: no pomóżcie mi to rozwiązać

5-latek: Ale czasem trzeba myslec ci sie pisze Jesli ma byc symetralna to nie moze przechodzic przez dwa rozne punkty odcinka tak jak napisal PW tylko przez konkretny punkt a my wiemy jaki (srodek odcinka ) i jeszcze do tego ma byc do tego odcinka prostopadla . I to nie jest zadne gowno tylko zadanie od ktrorego moze zalaec ocena jaka dostaniesz Teraz policz wspolrzedne srodka odcinka |AB| . masz na to wzor .

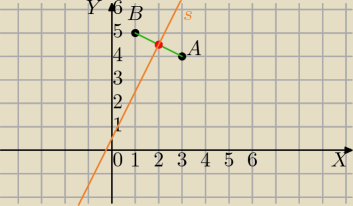
Mila: A=(3,4) B=(1,5) Nati ,po pierwsze bez nerwów, po drugie rysunek. (I )sposób , jak u Camusa a) środek AB

	3+1
xs=		=2
	2

	4+5
ys=		=4,5
	2

S=(2; 4,5) Patrz rysunek b) równanie prostej AB ( tylko wsp. a) y=ax+b 4=3a+b

	−1
5=a+b odejmuję stronami: −1=2a⇔a=
	2

	−1
y=		x+b
	2

symetralna odcinka AB jest do AB prostopadła⇒

	1
s: y=2x+b i S∊s⇔4,5=2*2+b ⇔b=
	2

	1
s: y=2x+
	2

Drugi sposób Symetralna odcinka jest zbiorem punktów jednakowo odległych od końców odcinka P(x,y) − punkt symetralnej AB √(x−3)²+(y−4)²=√(x−1)²+(y−5)² /² x²−6x+9+y²−8y+16=x²−2x+1+y²−10y +25 −6x−8y+25=−2x−10y+1+25 2y=4x+1

	1
y=2x+
	2

natii: dziękuję

Mila: