Funkcja logarytmiczna amatormatmy: witam, jak mam rozwiązać: f(x)=log ¹₅ [(x+5)(3x−6)]. Męczę się z tym, ale nie mogę tego zrobić. Pytałem na innych forach, ale nie potrafią mi tego wytłumaczyć. Pomocy

Kaja: ale jakie dokładnie jest polecenie?

Eta: Co masz obliczyć? bo nie napisałeś?

amatormatmy: sorki, chodzi o wyznaczenie dziedziny

Kaja: (x+5)(3x−6)>0 x∊(−∞;−5)∪(2;+∞) zatem D=(−∞;−5)∪(2;+∞)

Eta:

	1
Czy podstawą logarytmu jest		?
	5

D: (x+5)(3x−6)>0 /:2 ⇒ (x+5)(x−2)>0⇒ x€ (−∞, −5)U (2,∞)

amatormatmy: wielkie dzięki. zastanawiam się jedynie kiedy (w jakich przypadkach) należy zaznaczyć że dziedzina ma te nieskończoności?

amatormatmy: eta: tak

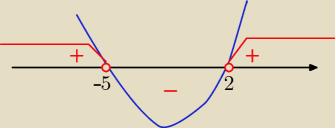
Eta: (x+5)(x−2)>0 −−−− to nierówność kwadratowa

Eta: https://matematykaszkolna.pl/strona/93.html

amatormatmy: mam jeszcze jedno pytanie (mam pewne braki co do funkcji logarytmicznej), mianowicie pamiętam że funkcja ta miała własności takie że nie "dotykała" osi OY i przecinała oś OX w miejscu (1;0). pytanie dlaczego w funkcji logarytmicznej rysujemy kwadratową? co jest istotą tej funkcji?

krystek: https://matematykaszkolna.pl/strona/217.html

Kaja: zakładamy, że liczba logarytmowana jest większa od zera czyli własnie tu (x+5)(3x−6)>0. a więc do rozwiązania jest taka nierówność, stąd parabola.

Kaja: bo wykresem lewej strony tej nierówności jest właśnie parabola o miejscach zerowych −5 i 2

amatormatmy: właśnie policzyłem sobie deltę do tego przykładu i wyszło mi że x₁=−2 a x₂=5. co zrobić aby te minusy wyszły mi poprawnie?

Kaja: byc może źle cos policzyłeś. sprawdź swoje oblioczenia

amatormatmy: aaj. zapomniałem o minusie. w takim razie wszystko w porządku

Kaja:

amatormatmy: mam jeszcze taki przykład f(x)=8 ^3x+2_x (ułamek jest potęgą). czy rozwiązaniem będzie x>− ²₃?

Eta: D_f : mianownik ≠0 ⇒ x≠0 D_f= R\{0}

amatormatmy: czyli w tego typu przypadkach pod uwagę bierzemy wyłącznie mianownik?

Eta: tak , jak wyrażenie wymierne !

amatormatmy: a tu: f(x)=(x+2)⁻³ ?