Oblicz długość wysokości oraz środkowych trójkąta
wajdzik: Oblicz długość wysokości oraz środkowych trójkąta o wierzchołkach:
A=(−1,3) B=(−4,0) C=(1,2)
| | xA+xB | | yA+yB | | 5 | | 3 | |
SAB=( |
| ; |
| )=(− |
| ; |
| ) |
| | 2 | | 2 | | 2 | | 2 | |
| | xB+xC | | yB+yC | | 3 | |
SBC=( |
| ; |
| )=(− |
| ;1) |
| | 2 | | 2 | | 2 | |
| | xA+xC | | yA+yC | | 5 | |
SAC=( |
| ; |
| )=(0, |
| ) |
| | 2 | | 2 | | 2 | |
|AS
BC|=

WIem, że mam teraz obliczyć długości środkowych w trójkącie ABC ale [C[TOTALNIE NIE WIEM JAK TO
ZROBIĆ.]] Próbowałem różnych wzorów ale mi nic nie chce wyjść. Proszę o pomoc.
9 cze 19:45
Eta:
Nie wierzę



!
wzór na długość odcinka!
|CS
AB|=
√(xS−xC)2+(yS−yC)2=..........
9 cze 19:48
Tadeusz:
... to odpowiedz sobie na pytanie co to jest środkowa −

9 cze 19:49
wajdzik: chwila moment, ale nie mam przecież ani xS ani yS?
9 cze 19:54
wajdzik: nie ogarniam ....
9 cze 19:56
wajdzik: Eto, czemu jest tak jak napisałaś a nie tak:
|CSAB|=√(xB−xA)+(yB−yA)2?
9 cze 20:00
Eta:
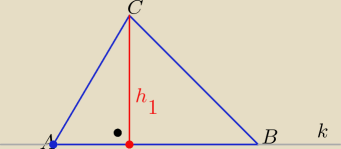
Można np; tak
| | yB−yA | |
wsp. kierunkowy ak= |
| = ..... = 1 |
| | xB−xA | |
k: y= 1(x−x
A)+y
A ⇒ k: y=x+4
k: x−y+4=0
d −−− odległość wierzchołka od prostej k
| | |1−2+4| | | 3 | |
h= d(C,od prostej k)= |
| = |
| = 1,5√2 |
| | √2 | | √2 | |
| | 2P | | 2P | |
h2= |
| =.... i h3= |
| =.... |
| | |BC| | | |AC| | |
9 cze 20:01
Eta:
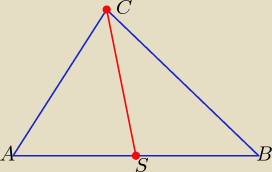
|CS|=
√(xS−xC)2+(yS−yC)2
9 cze 20:04
wajdzik: | | 3√2 | |
jeśli obliczyłaś hC= |
| to albo gdzieś się pomyliłaś albo mam błąd w wynikach w pdr. |
| | 2 | |
| | √2 | |
Wynik z podręcznika: |
| |
| | 2 | |
9 cze 20:14
Eta:
Sprawdzałam : wysokość poprowadzona z wierzchołka C do podstawy AB
Sprawdź czy dobrze podałeś współrzędne wierzchołków?
9 cze 20:20
wajdzik: Tak jest, są podane prawidłowo. Ale dość często mam tam błędy.
Druga sprawa. To co na początku wyliczyłem(współrzędne), S
AB S
BC.. to mi się przyda w tym
zadaniu?
I jeszcze jedno, bo widziałem, że mam obliczyć |AB|, czyli muszę policzyć:
|AB|=
√(xB−xA)2+(yB−yA)2 
?
9 cze 20:24
Eta:
tak

9 cze 20:30
9 cze 20:30
wajdzik: |AB|=
√18
| | 1 | | 1 | | 3√2 | | 1 | |
PΔABC= |
| *|AB|*h1= |
| *3√2* |
| = |
| [j2] |
| | 2 | | 2 | | 2 | | 4 | |
9 cze 20:37
wajdzik: I jak to wygląda

9 cze 20:37
wajdzik: 
9 cze 20:43
wajdzik: 
9 cze 20:56
5-latek : | | 1 | | 18 | |
3√2*3√2=18 * |
| = |
| =..... pole |
| | 4 | | 4 | |
9 cze 21:01
9 cze 21:02
wajdzik: Nie służy mi nauka całodniowa. Z godziny na godzinę coraz gorzej.
Dobra, dokończę jeszcze te dwie wysokości i pola i koniec na dzisiaj, dzięki wielkie.

9 cze 21:03
5-latek : A po co caly dzien . Czy poprawiasz ocene ? Musisz byc wypoczety

9 cze 21:21
wajdzik: Nie poprawiam, po prostu miałem zaległości bo na wycieczce byłem 3−dniowej i muszę:
raz.nadrobić materiał, 2.Uczyć się na sprawdzian który jeszcze nie pisałem(geometria na
płaszczyźnie), uwielbiam liczyć a geometria to moja słabsza strona i tymbardziej się do niej
przykładam.

9 cze 22:45
 WIem, że mam teraz obliczyć długości środkowych w trójkącie ABC ale [C[TOTALNIE NIE WIEM JAK TO
ZROBIĆ.]] Próbowałem różnych wzorów ale mi nic nie chce wyjść. Proszę o pomoc.
WIem, że mam teraz obliczyć długości środkowych w trójkącie ABC ale [C[TOTALNIE NIE WIEM JAK TO
ZROBIĆ.]] Próbowałem różnych wzorów ale mi nic nie chce wyjść. Proszę o pomoc.


 !
wzór na długość odcinka!
|CSAB|= √(xS−xC)2+(yS−yC)2=..........
!
wzór na długość odcinka!
|CSAB|= √(xS−xC)2+(yS−yC)2=..........

 Można np; tak
Można np; tak
 |CS|= √(xS−xC)2+(yS−yC)2
|CS|= √(xS−xC)2+(yS−yC)2
 ?
?






