Napisz równania: wajdzik: Punkty A=(−2,3), B=(4,7), C=(8 −2) są wierzchołkami trójkąta ABC. Napisz równania: a)prostych zawierających wysokości tego trójkąta, b)symetralnych boków trójkąta. Nie za bardzo wiem jak zacząć to zadanie Z góry dziękuję za pomoc.

PW: Wektor AB^→= [4−(−2), 7−3]=[6, 4] jet prostopadły do wysokości przechodzącej przez C, równanie tej wysokości ma więc postać ogólną Kx+Ly+M=0, gdzie K i L to ... (patrz współrzędne wektora).

wajdzik:

	yA−yC		3+2		5		1
aAC=		=		=		=−
	xA−xC		−2−8		−10		2

a*a₁=−1

	−1		2
a1=		=−1*(−		)=2
	−0,5		1

y=a₁(x−x_B)+y_B=2(x−4)+7=2x−8+7=2x−1 Co powiecie na tą część zadania? ok?

wajdzik: To jest źle. Ale mam jakiś trop, zaraz wrzucę.

wajdzik: wziąłem się za b) najpierw: a więc symetralna AB A=(−2,3) B=(4,7), C=(8,−2)

	3
a1=? Nie wiem od czego to zależy w tym momencie. Przypuszczam, że jest
	7

	7
an'=−
	3

	7
y=−		x+b
	3

	−2+4		3+7
środek AB S1=(		;		)=(1,5)
	2		2

	7
5=−		+b
	3

	1
b=7
	3

	7		22
y=−		x+
	3		3

Mógłby ktoś powiedzieć co robię źle?

	3		13
Wynik ma być taki: AB: y=−		x+
	2		2

bezendu: poczekaj zaraz napiszę swoje obliczenia wyszło mi tak jak w odpowiedziach

bezendu: prosta przechodząca przez punkty A i B −2a+b=3 /(−1) 4a+b=7 2a−b=−3 4a+b=7 6a=4

	2
a=
	3

	2
4*		+b=7
	3

	13
b=
	3

	2		13
prosta ta ma postać y=		x+
	3		3

prosta prostopadła i przechodząca przez punkt S=(1,5)

2
	*a=−1
3

2
	a=−1
3

	3
a=−
	2

	3
y=−		x+b
	2

przechodzi przez punkt S (1,5)

	3
−		*1+b=5
	2

	3
b=5+
	2

	13
b=
	2

	3		13
y=−		x+
	2		2

PW: A nie znasz tego twierdzenia, o którym napisałem na początku, że w równaniu ogólnym prostej współczynniki przy x i przy y są współrzędnymi wektora prostopadłego do prostej? Wektor [ K, L ] jest prostopadły do prostej Kx+Ly+M=0. Rozwiązanie jest wtedy króciutkie: liczysz K i L, potem podstawiasz do równania Kx+Ly+M=0 współrzędne wierzchołka C i po robocie.

bezendu: sposób PW o wiele prostszy ale skoro nie znasz tego wzoru to musisz tradycyjnie robić to zadanie

wajdzik: Panowie, ten sposób jest prostszy, tak słyszałem. Ale na jutro muszę się nauczyć ogólnie a tego twierdzenia jeszcze nie ogarnąłem i w tym problem.

wajdzik: PW, mógłbyś mi przedstawić sposób z tego twierdzenia? Bo czas mnie goni a mam jeszcze multum zadań.

bezendu: Masz tablice maturalne 6 strona od samej góry są te wzory

wajdzik: już sobie ściągnę.

wajdzik: bezendu, Ty obliczyłeś tylko symetralną AB wcześniej tak?

bezendu: Tak, przecież nie będę za Ciebie wszystkiego liczył

wajdzik: Tylko się upewniłem spokojnie, poza tym rozgryzam ten krótszy i lepszy sposób, już wrzucam.

bezendu: robiłeś tym sposobem więc zrobiłem tym samym poprawnie i teraz wiesz gdzie masz błędy

wajdzik: A więc: AB^→[(4+2)7−3)]=[6,4] 6x+4y+M=0 4y=−6x−M

	3		3
y=−		x−{M}{4} a=−		Tutaj to a mi już niby wyszło ale dalej to coś mieszam.
	2		2

	3
y=−		x+c
	2

−2=−12+c c=10 Co robię źle?

bezendu: https://matematykaszkolna.pl/strona/1213.html przeczytaj ze zrozumieniem i jeszcze raz rozwiąż

wajdzik: Zrobiłem pewnie błąd przy tym M gdzie dałem do mianownika 4. Ale totalnie nie mam pojęcia jak mam z nim tutaj, że tak powiem "współpracować"

wajdzik:

wajdzik:

wajdzik:

wajdzik: Symetralne obliczone, mógłby ktoś pomóc przy a)prostych zawierających wysokości tego trójkąta,

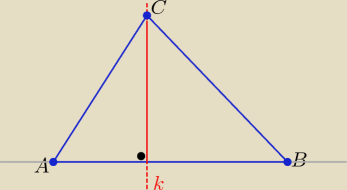
Eta: np: k ⊥AB i C€ k

	yA−yB
k: y= aAB(x−xC)+yC , aAB=		dla xA≠ xB
	xA−xB

y=......... podobnie pozostałe równania wysokości

Eta: Sorry oczywiście ma być:

	1
k: y= −		(x−xC)+yC
	aAB

wajdzik:

3−7		−4		2
	=		=
−2−4		−6		3

	3
y=−		(x−xC)+yC
	2

	3
y=−		x+10
	2

	3
−		x−y+10=0
	2

Jedno się zgadza, postaram się zrobić resztę. Dzięki Eto

Eta:

wajdzik: Wszystkie wyniki poprawne, wszystko zrozumiałem. DZIĘKUJĘ!

Eta: I tak trzymaj