. asdf: Witam, pomozecie? http://postimg.org/image/ev1bu0n4h/ Musze zrobic te zadania, nie są one trudne, ale na prawde − jestem zawalony robotą od kilku dni...moglibyscie to rozwiazac? Nie wyrabiam w czasie

Kostek: @asdf tu masz 3 https://matematykaszkolna.pl/forum/205499.html

asdf: dzieki bardzo

aniabb:

	x2
y=
	1+x2

	2x(1+x2)−x2•2x		2x+2x3−2x3		2x
y' =		=		=
	(1+x2)2		(1+x2)2		(1+x2)2

	2(1+x2)2−2x•2•(1+x2)•2x		2(1+x2)2−2x•2•(1+x2)•2x
y'' =		=
	(1+x2)4		(1+x2)4

aniabb:

	2−6x2
y''=
	(1+x2)3

punkt przegięcia y''=0 2−6x²=0 x1= √3/3 lub x2= −√3/3 pomiędzy funkcja wypukła (−√3/3 ; √3/3 ) poza funkcja wklęsła (−∞;−√3/3) u ( √3/3;∞)

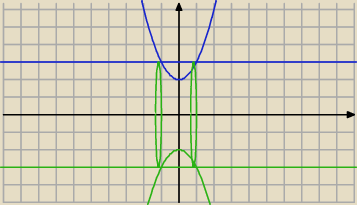
Vizer: 2. Widać, że należy tu obliczyć objętość walca powstałego przez y = 3 i odjąć od niego objętość "resztki", która wycięła parabola. Punkty przecięcia : x² + 2 = 3 x² = 1 x = 1 v x = −1 V = 2π( ∫¹₀ 9 dx − ∫¹₀ (x⁴ + 4x² + 4) dx) =

	1		1
= 2π([9x]10 − [		x5 + 4 *		x3 + 4x]10) =
	5		3

	1		4		83		52		104
= 2π(9 − (		+		+ 4)) = 2π(9 −		) = 2π *		=		π
	5		3		15		15		15

Jeśli się gdzieś nie walnąłem w rachunkach

asdf: dzieki

asdf: czemu tam jest 2π ?

Vizer: Zrobiłem to dla ułatwienia. Bo jak widzisz granice całkowania mam od 0 do 1 (normalnie powinny być od −1 do 1), więc liczę połowę właściwej objętości, dlatego też wszystko mnożę jeszcze razy 2.