skalar joanna: Wiedząc, że p^→ oraz q^→ są prostopadłe oraz x^→ = 3p^→ − 2q^→ i y^→ = p^→ − 5q^→ wylicz iloczyn sklarany x^→ oraz y^→.

Aga1.: x^→oy^→=(3p^→−2q^→)o(p^→−5q^→)= 3(p^→)²−15p^→oq^→−2p^→oq^→+10(q^→)²=3(p^→)²−15*0+2*0+10(q^→)²=3*1+0+0+10*1=13 Objaśnienie wektory p i q są prostopadłe, więc ich iloczyn skalarny jest równy 0, oraz jednostkowe wiec ich długość wynosi 1.

Janek191: → → → → p oraz q są prostopadłe, więc p o q = 0 oraz → → → → → x = 3 p − 2 q i y = p − 5 q zatem → → → → → → x o y = ( 3 p − 2 q ) o ( p − 5 q ) = → → → → → → = 3 ( p )² − 15 p o q − 2 q o p + 10 ( q )² = = 3 p² − 15*0 − 2*0 + 10 q² = 3 p² + 10 q² ======================================= bo → → p o p = p * p = p² → → → → p o q = q o p → → gdzie p = I p I , q = I q I → → p , q − długości wektorów p i q

Janek191: @Aga1 → → Gdzie jest napisane , że wektory p , q są jednostkowe ?

Aga1.: @ Janek191 Masz rację, jest napisane,że wektory p i q są prostopadłe.

joanna: dziękuje za rozwiązanie a jak wyliczyć dł. wektora x^→ = 5p^→ − 4q^→, wiedząc, że p^→ oraz q^→ są prostopadłe?

aniabb: z pitagorasa |x|= √(5p)²+(4q)²

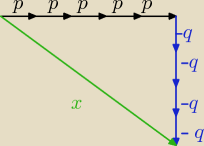
aniabb: np.

joanna: ale jak to obliczyć?

aniabb: o 11:43 masz wzór

joanna: to widzę, ale co podstawić za p i q ?

Janek191: → → Za p długość p, a za q długość q

aniabb: a co podstawiałaś licząc iloczyn skalarny?

joanna: czy wychodzi na to, że długość to: |x| = √25p² + 16q²

joanna:

aniabb: tak

joanna: dziękuję a jak mam podane w takiej postaci: obliczyć x^→ który ma dł. 1 i jest prostopadły do a^→ = [1, −2, 0] oraz b^→ = [0, 3, −2]

aniabb: [4/√29 ; 2/√29 ; 3/√29 ]

aniabb: liczysz wyznacznik z danych wektorów i wektora i,j,k ( jako wersorki) a potem dzielisz przez długość

joanna: wyznacznik z tylko dwóch wektorów ? wyznacznik nie powinien być kwadratowy ?

aniabb: | i j k | | 1 −2 0 | = 4i + 2j + 3k czyli [ 4 ; 2 ; 3 ] | 0 3 −2 | a ponieważ jego długość jest √29 to jak wyżej (12:19)

pigor: ..., może np. tak : iloczyn wektorowy danych wektorów jest ⊥ do nich I i j k | a^→ x b^→= |1 −2 0 | = 4i+0j+3k−0k+2j−0i= 4i+2j+3k= [4,2,3}, a jego długość |0 3 −2 | |a^→ x b^→|= √16+4+9= √29, więc

	4		2		3
x→= [		,		,		]=129√29 [4,2,3] − szukany wektor
	√29		√29		√29

joanna: czego długość jest √29 − wektora [4, 2, 3] ?

aniabb: tak

aniabb: a w zadaniu chciałaś by miał długość 1 więc trzeba go skrócić przez √29 zachowując kierunek

joanna: ok, dziękuję to mam ostatnie zadanie też muszę obliczyć x^→ o dł. 1, który razem z i^→ = [1, 0, 0] oraz j^→ = [1, √3, 0] tworzy

	π
kąt
	3

aniabb: [ 1/2 ; √3/3 ; 2/3 ]

aniabb: https://matematykaszkolna.pl/strona/1630.html

joanna: tylko, że otrzymam wtedy:

	π		i→ ◯ j→
cos		=
	3		|i→| * |j→|

a jak wyliczę x^→

joanna:

joanna:

joanna:

joanna:

B: Co za matoły........

aniabb: za i^→ wstawiasz szukany x czyli np [a;b;c] a za j^→ jeden z danych ..potem to samo robisz z drugim a potem z tego że długość ma być równa 1 wyliczasz c

joanna: j^→ = [1, √3, 0] x^→ = [a, b, c] wtedy otrzymam:

1		a + √3b
	=
2		4a2 + 4b2 + 4c2

4a² + 4b² + 4c² = 2a + 2√3b dobrze?

joanna: drugie a + √3b = 4a 3a = √3b

	√3
a =		b
	3

i co dalej ?

joanna: dobrze

joanna:

joanna:

joanna:

aniabb: Długość x z założenia jest 1 więc w mianowniku masz 1

joanna: czyli:

1		a + √3b
	=
2		4

1		a
	=
2		4

a + √3b		a
	=
4		4

a + √3b = a √3b = 0 gdzie popełniłam błąd ?

Aga: https://matematykaszkolna.pl/forum/205535.html proszę o pomoc

joanna:

a + √3b
	= a
4

a + √3b = 4a czyli:

	√3
a =		b
	3

czyli to co otrzymałam, tylko jak to dalej obliczyć ?

aniabb: z wektorem [1,0,0]

1		a+0+0
	=		więc a=1/2
2		1

z wektorem [1,√3,0]

1		a+√3b+0
	=		więc b=√3/6 na górze miałam literówkę
2		2

i z długości c a²+b²+c²=1 więc c=2/3